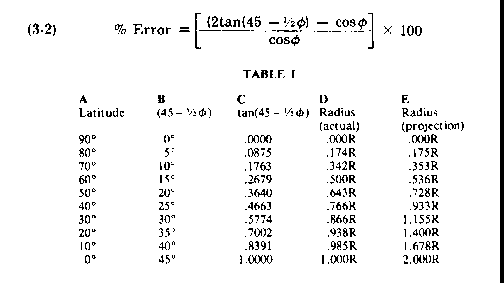

Substituting the values from Table I into Equation 32,.., we get the percentage of error for the 9 circles of latitude and the North Pole, as in Table II below. Column B gives the percentage of error for a projection on a tangent plane at the North Pole. Column C gives the percentage of error for a tangent plane at 60° north latitude. This is of course the standard latitude used in the construction of most weather maps. Column C was obtained by subtracting 7.18 % from the values in Column B.
The stereographic map possesses the important property that shape is preserved at a point, since every point is stretched equally in all directions like any point on the surface of a rubber balloon. If a face is painted on a round rubber balloon, we will see the same face when the balloon is blown up, but larger in size. The point at the tip of the nose (and all other points) is stretched equally in all directions. We still have
the tip of a nose in the larger blown up version, but the tip occupies more area. Figure 3-8 has been drawn to give a clearer visual picture of this type of distortion on the weather maps used as examples in this book.
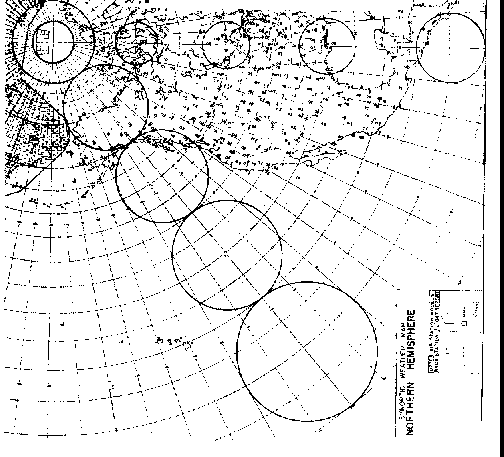
Figure 38. Above is a partial polar stereographic map with two sets
of circles, one with a radius of 5°, and the other with a radius of
10°. One circle for each radius is centered at the North Pole, 70°,
50° 30°, and 10° latitude.
On the surface of the Earth, all circles of equal radius are perfect circles, and each one covers the same area. Obviously, Figure 38, seems to contradict this fact. The error in this figure is created by the map projection, and the amount of error in the size of the circles can be calculated with the aid of Equation 32, as has been done in Table II.
The Irregular Appearance of the Projection of the Centers of Circles
The drawing of Figure 3-8 requires the proof of two separate facts: First, does any circle on the surface of the Earth project as a perfect circle on the map; and second, does the center of the circle on the Earth become the center of the circle on the flat map? Surprisingly, circles on the Earth always show up as circles, parts of circles, or straight lines, on the flat map, but the centers do not match up. What follows is the standard proofs for these conclusions.
In Figure 3-9, the small circle diameter xy projects into XY and the small circle's center c into C; since the South Pole, S. is the point of projection. P is the middle point between X and Y. We can see that there is a difference between C and P. due to the distortion of length caused by the projection. Therefore, xc and cy will not project as equal lengths, even though they are equal on the surface of the Earth. The true center of the circle lies closer to the North Pole on the polar stereographic map than the center of the projected circle (it lies closer to the South Pole in the Southern Hemisphere).
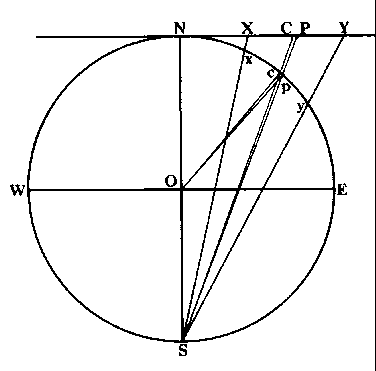
Figure 39. The diameter, xy, of a circle on the surface of the Earth, is projected with a diameter of XY, onto the tangent plane. The center of a circle, c, is projected as C on the plane. Strangely, the center of the projected diameter is P. not C (which is the projection of the original center, c).
All Circles on the Earth's Surface Project as Circles on the Map
Now let us prove that all circles on the surface of the Earth show up
as circles on the stereographic map. In 3-10, let WGEF be the equatorial
circle (also called the primitive circle) of a sphere with N
and S as the poles, and with pole S as the point of projection. Let P1
be any point on the sphere. We will find that a plane through the points
of the great circle NP1GS will intersect the equatorial plane in a straight
line GOF. The polar distance of a point on the sphere is its angular
distance on the surface of the sphere from one of the poles of the equatorial
circle. Therefore, the arc NP1 is the polar distance of P1 . The magnitude
of the angle of NP, is determined by the angle NOP1 . p1 is the stereographic
projection of point P1 in the equatorial plane, since p1 is the point in
which SP1 pierces the equatorial plane. Since P1 was chosen in the Northern
Hemisphere, its projection is inside the Equatorial Circle. If P1 had been
chosen as a surface point in the Southern Hemisphere, then the projection
point of P1 would have been outside the Equatorial Circle. 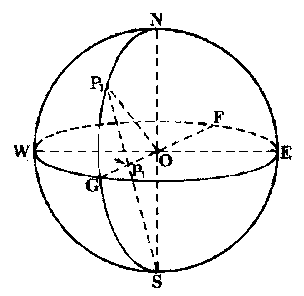
.
Figure 3-10. See the text for the explanation.
In Figure 3-11, WGEF is again the Equatorial plane, with N and S as the poles of the sphere. Let QQ1R be a small circle on the sphere. The pole P of the small circle is at the end of the radius OP of the sphere. This radius OP is perpendicular to the plane of QQ1R. The polar distance of a circle is the angular distance of any point on its circumference from either one of its two poles (the second pole, which is not shown, is diametrically opposite to pole P). The polar distance of the small circle is PQ, which also equals PR. The inclination of a circle is the angle between its own plane and the Equatorial plane. The inclination of the small circle plane
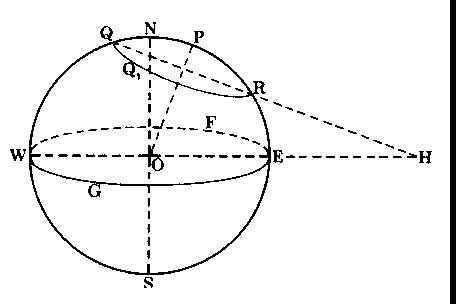
Figure 3-11. See the text for the explanation.
QQ1R to the Equatorial plane WGEF is the angle RHE, which is also measured by the arc NP. NP1 of course, is measured by the angle NOP, which exists between the pole of the equatorial plane and the pole of the small circle. The points N, O, and P lie in a plane, which intersects the Equatorial plane along the line WOE. This line, WOE, is called the line of measures of the circle QQ1R.
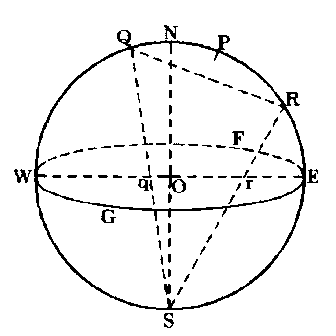
In Figure 3-12, we show how the end points Q and R of the small circle (shown in Figure 3-11) project onto the Equatorial plane. We see that R projects as point r, and Q projects as point q, on the line of measures, WOE, in the Equatorial plane.
In Figure 3-13, below we let Pc be the vertex of a cone tangent to the sphere along the circumference of the small circle QQ1R. (only the front half of the circle is shown), with the lines PcQ and PcR representing the extremities of the cone. The curve qq1r represents the projection in the equatorial plane of the small circle QQ1R. By connecting all the points
in the small circle QQ1R with the center of projection S. we form another
cone with SQ and SR at the extremities. Pc as a vertex projects into the
equatorial plane as the point Pc. 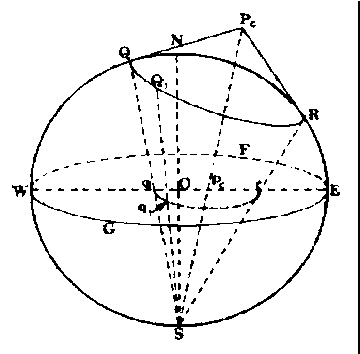
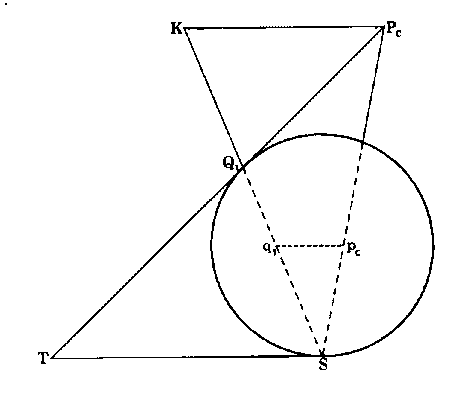
In Figure 3-14, below the points S. Q1, and Pc lie in a plane. This plane cuts the equatorial circle in the line pcq1 which is the projection of the line PcQ1 of the cone. We draw a tangent line to the point S that is also in
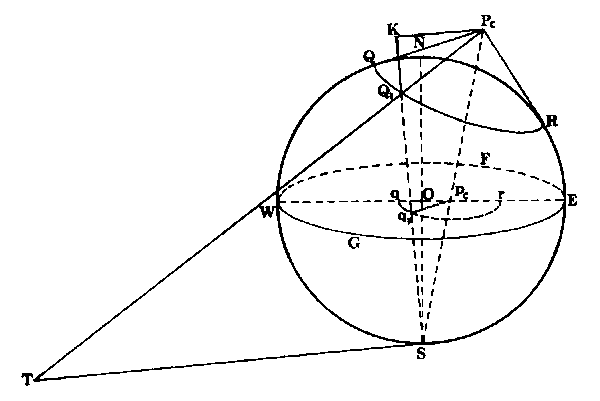
the same plane as SQ1Pc. We extend the line from PcQ1 to the point T where it crosses the tangent line from S. The line SQ1 is a chord of the sphere since the points S and Q1 are both on the surface of the sphere. The line ST is parallel to pcq1, since the plane tangent at point S is also parallel to the equatorial plane in which pcq1 lies. In this figure, pcq1 does not look parallel because the figure is shown in perspective. In an actual threedimensional sphere the parallelism would be easily seen. We draw PcK parallel to TS and extend the line Q1S to where it meets the line from Pc at point K. The points S. T. Q1, K, and Pc all lie in the same plane.
In Figure 3-15, below we see another view of the plane (STQ1KPc) and how it cuts the sphere. Since PcK and TS are parallel, the alternate interior angles TSQ1, and Q1KPc are equal. TS and TQ1 are tangents from the common point T. so they are equal, and the angle TSQ1 = angle TQ1S = angle KQ1Pc. Therefore PcK = PcQ1. The triangles Sq1Pc and SKPc, are similar,
pcq1 = pcq1 = pcS or pcq1 = PcQ1 x pcS
PcK PcQ1 PcS PcS
which is equal to a constant, since PcQ1, pcS and PcS are all fixed lengths that can not change when we move to different points on the small circle.
Since pcq1 is constant, and since the point pc is fixed; the locus (path) of q1 (which follows Q1, as Q1 goes around the small circle) is a circle where the center is the projection pc of the vertex Pc of the tangent cone-which is what we set out to prove.
The Value of the Angle Between any two Arcs on the Surface of a Sphere is Exactly Reproduced on the Polar Stereographic Map
In Figure 3-16, below, two arcs Y1 and Y2 meet at a point P on the sphere. These two arcs project as y1 and y2 onto the equatorial plane which is used as the plane of projection. A plane tangent to the projection point S is also parallel to the equatorial plane. In this figure, the tangent lines PV and PT are projected as pV and pT onto the equatorial plane (with the longest parts of the lines outside of the equatorial circle). Now since triangle QSRiS in the tangent plane that touches point S. the line QS and RS are tangent to the sphere. Two lines (QS and QP) from point Q are tangent to the sphere at points S and P; in a similar manner, two lines (RS and RP) from point R are also tangent at points S and P. Therefore, in the two triangles QSR and QPR, we find that QR is common to both triangles, while QS = QP, and RS = RP (since any two lines that are tangent to a sphere from a fixed point outside the sphere are always equal in length). Consequently, angle QSR = angle QPR = angle VpT.
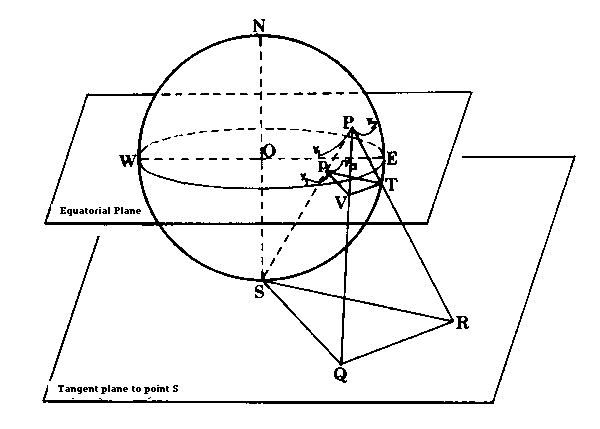
The angle between the two curved arcs that cross on the sphere, Y1 and Y2 in Figure 3-16, is measured by the angle QPR between their tangent lines, PQ and PR, at the point of intersection of the arcs. Likewise, the angle between the two projected arcs, y1 and y2 is the angle VpT between the projected tangents pV and pT. Therefore, when any configuration on the sphere is projected, we find all the angles unchanged in the projection.