While investigating the various tones of music, Ernst Chladni (1756-1827) made a classic experiment to show the effects of harmonic vibrations. He spread fine sand over a glass or metal plate and set it into vibration with the bow of a violin by scraping the bow along one edge of the plate. The bow would alternately stick and slip in rapid succession on the edge of the plate to create waves of sand (also sound waves). He would hold the plate between his fore finger and thumb; the point where the plate is held is, of course, a node where there can be no movement. The bow sets up waves that move across the plate and then are reflected from the edges. The reflected waves become superimposed on the new waves coming from the bow edge. This results in symmetrical patterns of nodal lines where the plate is not moving. Figure 91 shows square and circular plates that are being held in the center. The type of pattern created depends generally on:

91

the point or points of support and their location; the point where the bow is touched to the plate; the frequency of the vibration which is influenced by the speed the bow is moved; and the properties of the plate itself, such as thickness, volume density, elastic strength, etc.

The symmetry of the Chladni figures is partially determined by the symmetry of the plates chosen. A circular plate can have an infinite number of symmetry lines through the center.

The plate acts like a cymbal or drum and breaks up into vibrating parts separated by the lines which do not move. This is an example of stationary vibration. All the points on one side of a line are moving in opposite direction from the points on the other side of the line (up and down). The sand slides off the moving parts and gathers along the nodal lines.

Two Modes of Vibration

The vibrations of a twodimensional system can be broken down into two different systematic, types of modes. First, if we consider a circular plate, there can be a set of nodal diameters that will give one type of symmetry, as in Figure 9-2. In this example, the nodal diameters divide the circular plates into 4, 6, and 8 sectors to give what is known as the circumferential wavenumber of 4, 6, 8. Theoretically, the number of diameters can increase to 5, 6, 7, 8, and on to infinity, unless there are restraining forces to prevent a large number of diameters.

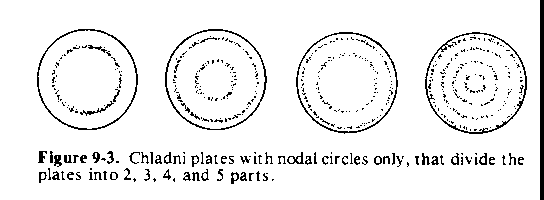
Second, there can be a set of nodal circles, to give another type of symmetry, as in Figure 9-3. Nodal circles divide the circular plate into 2, 3, 4, 5, 6, etc. rings, to give what is the radial wavenumber of 2, 3, 4, 5, 6, etc.

We can also have nodal diameters and circles occuring simultaneously as shown in Figure 94.

92

As a matter of interest, Figure 9-5 shows a threedimensional perspective view of some of the patterns of vibration of a clamped circular plate used in telephone receivers and small condenser microphones.

93

What we see on the Chladni type plates is none other than the same phenomena described by wavenumber earlier in Figure 5-2. This time, however, we have two separate wavenumbers operating simultaneously: the circumferential wavenumbers represented by Figure 9-2; and the radial wavenumbers (nodal circles) shown by Figure 9-3. In addition, the Chladni plates are nothing but another manifestation of Plateau's surfaces of revolution. The different, three dimensional shapes that form on a flat circular plate behave in a similar manner, even though different forces are involved. In this case however, the plates do not break up into small drops due to the high tensile strength of the materials of which it is constructed.

The phenomena that we associate with weather, such as winds, clouds, precipitation, etc., take place in a relatively thin film of air above the surface of the Earth. This thin film of air resonates in a manner similar to the vibrating Chladni plates. At any given time of the year, there is an equatorial belt insulating some of the weather activity in one hemisphere from the weather activity in the other hemisphere. Therefore, we will analyze only one hemisphere, the Northern hemisphere, due to the Equatorial separation in some of the weather effects, and due to the lack of data, and in order to simplify this first presentation, ever, of the charts shown in the latter part of this book.

Some Differences between the Hemispheric Cap of Air and Chladni Plates

A disturbance set up along the circumference of a circular Chladni plate will propagate automatically to the diametrically opposite side. This serves to prevent odd wavenumbers, since there is always a matching wave for any given wave, due to the stiffness of the metal plate, among other reasons.

The thin film of air over the Earth is not a flat, solid plate as in the Chladni experiments. The film of air in which the main weather phenomena take place is hemispherically shaped, immensely flexible or elastic, extremely mobile, and slippery. Therefore, a disturbance along the circumference of a group of geometrically related vortexes will not always propagate or show up as a resonant disturbance on the diametrically opposite side (you will see clusters of vortexes spaced in a circular arc around a central vortex, in the upcoming charts). This

94

means that odd wavenumbers of the type shown in Figure 9-6, are possible in weather phenomena. Nevertheless, there are many times when a disturbance on the circumference of a group of geometrically related vortexes will show resonant waves at a diametrically opposite end. This type of situation can be considered as occurring wherever we see three vortexes lined up in a straight line. The vortex in the middle can be considered as being the center of the geometrical configuration. We will see a number of these features in my chart series. 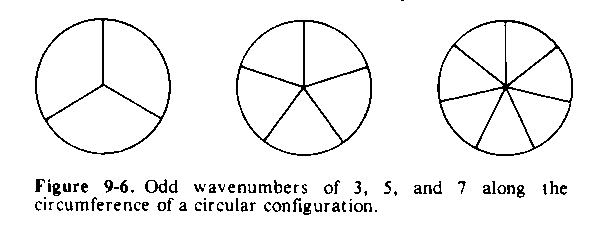95