
Chapter 7
Symmetry
A phenomena that permeates every nook and cranny of the Universe (similar to omnipresent waves)--is symmetry. First we will define symmetry and then show some of the most important classes of symmetry.
Definition of Symmetry
Any object is considered as being symmetrical when it consists of geometrically
and physically equal parts that are arranged relative to each other in
some kind of fixed order. The geometric equality must be a suitable
equality or a mirror image equality. A steel ball and a rubber
ball of the same size may be suitably equal, but they are not equal in
a physical sense. The right hand is equal to the left hand in all respects,
but the right hand can not be made to coincide with the left hand by placing
one hand over the other, unless one is reflected in a mirror. The right
and left hand have mirror equality. See Figure 7-1. A mirror image form
of the same symmetry is called enantiomorphism. 
Another condition of symmetry is that equal parts in any structure must always be arranged in a geometrically regular manner. It must be possible to divide the structure into an equal number of parts without any remaining odd shaped parts left over. In Figure 7-2, the scattered triangles become symmetrical as a group only after they have been arranged in an identical manner to form the hexagon.

Sometimes there can be a combination of different symmetries in one
structure. Figure 7-3 shows an octagon inside a square which is inside
a hexagon. Considered as a single unit, the figure is unsymmetrical, but
the three figures of which it is composed can be considered as being individually
symmetrical. 
Classes of Symmetry
According to A. V. Shubnikov and V. A. >Koptsik (8),
all symmetries in the Universe can be divided up into as many as 230 different
classes. For our purposes, there are three broad geometric classes. The
first is the point, which is usually associated with the mineral world.
The second is the line, which is usually associated with the plant domain.
The third is the plane, which is usually associated with the animal kingdom.
See Figure 74. 
A fundamental mineral form such as a star, a crystal, a soap bubble, etc., tend to be symmetrical around the point at their individual centers. The forces acting on these structures can operate equally in all directions.
Once any form of life attaches itself to the bottom of the sea or to the land (like a tree), a fixed up and down axis is generated. The bottom end with the roots is obviously different from the top end. There is no front or back or left or right for these life forms in either the sea or on the land. They generally take the symmetric form of a cone around the line of the vertical axis. Since the main controlling force is gravity acting along the up and down direction, things tend to spread out equally in all horizontal directions, like the branches of a tree, or water spreading out to form a horizontal surface in a lake, etc.
A moving animal is generally symmetric on either side of the plane that separates the right and left halves of its body. Due to environmental conditions, movements of up and down and forward and backward are all completely different. Moving in a forward direction, without the aid of a compass, can lead to veering to the right or to the left direction with statistically equal frequency--which accounts for the occurrence of bilateral symmetry about a plane with things like a right and left hand. In other words, an animal can see a predator (or food), in front, to the left, or to the right, so the animal's body is shaped to meet these directional challenges from the outer world. If a predator sneaks up from behind, he is in trouble and better run fast. . . Many of the manmade structures (like cars, chairs, etc.) have bilateral symmetry to serve man's own bilateral symmetry.
Types of Symmetry Operations
Using some of the definitions of crystallography (the science of crystals), we find that the point, the line, and the plane (as pictured in Figure 7-4) are called the symmetry elements. Every object possessing at least one symmetry element is symmetrical by definition. A symmetry operation is defined as any manipulation that may be performed on an object, after which the object itself appears to be exactly the same. The first symmetry operations we will consider are rotation and reflection.
The sphere is the most perfectly symmetrical figure iin three
dimensions. It can be rotated through any angle around any diameter, which gives it rotational symmetry; or it can be reflected in any plane, through the center, which gives it the symmetry of reflection.
The circle is the most perfectly symmetrical figure in two dimensions because it can be rotated around its center through any angle or reflected in any diameter. In three dimensions, the rotation is around an axis, while in two dimensions, the rotation is around a point. Any shape, other than spherical or circular that has rotational symmetry, can be broken up into symmetrical parts. There is always a smallest possible angle in which a pattern can be rotated and where the whole figure appears to be unchanged. For example, if the hexagon in Figure 7-2b is rotated around its center by 60° (which is the smallest possible angle), it will look exactly the same after the rotation is completed.
If a pattern can be rotated into 2 positions (half turn), it is called
a two fold or diad rotation. A rotation of 3 positions (one third turn)
is called three fold or triad, and 4 positions (quarter turn)
is a tetrad . . . the example of the hexagon and its 6 positions
is called a hexad. There is always a center point or center line in a symmetrical
pattern in a plane, as shown in Figure 7-5. In performing symmetry operations
of rotation or reflection, the center point or line remains fixed. 
There can be a single reflection line as in Figure 7-5a, which is the simplest kind. If there is more than one line of reflection, then there must also be a center point of rotation, since every reflection line must pass through the center of the figure. See Figure 7-6 for multiple axes of reflection.
A face from the front is a good example of symmetry about a line. See Figure 7-7. We call the line a mirror-line, and the left side of the face is a mirror image of the right side. Since a face is


three dimensional, we really have a mirror-plane rather than a mirror-line.
Let us now investigate the symmetry operation of translation. Translation,
as defined in crystallography, is the moving of a point from one location
in an object to some other location in the same object, while the environment
around the point remains the same. An example of a structure with translational
symmetry is a chain link fence as in Figure 7-8. If you found yourself
at point A or B. on any of the squares, everything would look the same
in all directions from those two points 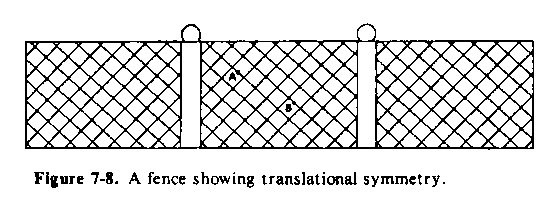
(locations). The operation of moving from point A to point B is called
a translation, and the fence has what is known as translational symmetry.
If we always move a whole number of spaces on the fence, everything
would appear exactly the same as at point A. However, moving from point
A by anything different than a whole number of spaces would result in the
fence looking different at that new point. It is possible for a pattern
to exhibit a combination of translational and reflectional symmetry simultaneously,
as shown in Figure 7-9. This kind of symmetry is called glide reflection.

Symmetry Along a Straight Line
What types of symmetry patterns can be found on both sides along a straight line? According to the laws of symmetry, there are only 7 possible symmetry patterns along a straight line on a plane surface. These are shown in Figure 7-10.
Dilation Symmetry
Dilation is the enlargement or reduction of a figure along lines radiating from a central point. See Figure 7-11 for samples of two dimensional patterns. There can be dilation along a straight line, as in Figure 7-12. There can be dilation with reflection, as in Figure 7-13. There can be dilation linked with rotation, as in Figure 7-14.
It is impossible to ignore the effect of dilation on any symmetry patterns that can be found on the polar stereographic weather map. In Figure 3-8, we can see a built in dilation, due to the way that the map is constructed.
Symmetry in a Network of Points
Let's turn for a moment to the definition of a crystal. It is a periodic repetition of a group of atoms at equal intervals throughout the volume

Figure 7-10. The 7 symmetry patterns that are possible along a straight line on a twodimensional surface.
a. Translation only-no rotation or reflection.
b. Halfturn of 180° (with the dot as the center of rotation) will give an identical shape.
c. Transverse reflection (with the dashed line showing the line of reflection or mirror).
d. Longitudinal reflection (where the straight line is the line of reflection).
e. A halfturn combined with both longitudinal and transverse reflection.
f. Glide (longitudinal translation) and reflection.
g. Longitudinal glide reflection, combined with transverse reflection and a halfturn around the points in between.



of the sample. As a result, the surroundings of any one of these groups is identical with that of any other group. An arrangement of points in space having the property that each point has identical surroundings of the same orientation is called a lattice.
You may be wondering how this applies to weather patterns. If you were to place a point at every high or low center on a hemispheric map,
you would have a rough network of points. You will find that the principles discovered about crystals have some interesting parallels in patterns on the surface weather maps, as will be shown in the charts later on.
Starting with a square network of points, we find it possible to draw
many different networks depending on the method used in connecting the
points, and also the total number of points used. See Figure 7-15. 
If the points are connected in such a way that only two straight lines cross at each point, then the area of each parallelogram formed is always the same as the area of one of the squares.
A network of points form what is known as a wall paper pattern,
which is a design that repeats itself at regular intervals in two directions
(for a plane surface). The simplest type is a row of dots repeating themselves
in parallel rows to form parallelograms, as in Figure 7-16. This kind of
wall paper pattern is called a net (network). 
These type of network patterns are encountered everywhere: in actual wall paper, in carpets, in crystals of course, in the tissues of plants and animals, in honeycombs, etc. In Figure 7-16, the length of the leg of the parallelogram is longer in the X direction than the leg in the V direction. In Figure 7-17, we make the length of the leg in the X direction and in the V direction of the parallelogram equal. This figure has more

symmetry elements, since it now includes reflection symmetry; the dashed
line represents one of the lines of reflection. Lastly, in Figure 7-18,
the angle between leg X and Leg Y is equal to 90°, and the length of
leg X equals leg Y. This adds rotational symmetry to the pattern, since
we can rotate leg X into leg Y with a 90° rotation for any small square.

There are only 5 types of parallelogram nets possible, each differing
from the other in symmetry. See Figure 7-19. In this figure, we have the
individual parallelograms formed by 4 separate points in 7-19a, b, c and
d; while e uses 5 points, with 4 for the corners and one occupying the
center. Two of the sides of a parallelogram are indicated as X and Y when
the sides meet at right angles, and as X and V when they meet al an angle
other than 90°. 
Equivalent Symmetry Points
There is one more aspect of symmetry that we must consider when we look
for symmetry patterns on a weather map. As an example, we will take a look
at the 4 fold symmetry of a square, as shown in Figure 720. This symmetry
is indicated by the 4 lines going through the 
center. We pick any point in the square that is not on one of the symmetry
lines (Figure 7-20a). We can see that there are 7 other points that can
be spaced in an equivalent or symmetric position (Figure 7-20b). If the
original point is now moved towards the center (Figure 7-20c), we will
find that the similar points will move to the center. All the points will
merge into the point at the center when the original point we chose moves
into the center. Now if we move the original point towards one of the symmetry
lines (Figure 7-20d), all the other points similar to the original point
will move towards the corresponding symmetry line. In this case, the total
number of equivalent points will be cut in half. The same type of analysis
can be applied to a triangle as in Figure 7-21, and to any other figure
with lines of symmetry. 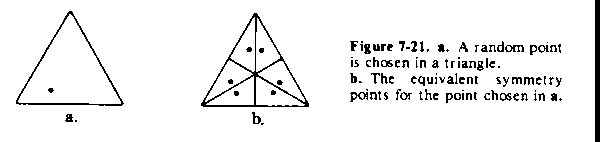
Symmetry of Averages
In Singer's Lock we are making calculations with a network of points (the centers of highs, lows, and cols). It is a matter of interest to
investigate many aspects of an array of points. In Figure 7-22a, we
show a square net of points which form a regular figure since each point
occupies a similar position with respect to other points. In Figure 7-22b,
we show a disorderly arrangement of points, but they have the same average
density. It can also be considered a regular figure in groups, if it is
divided into sections with approximately the same number of points. 
How Many Points Will be Crossed by any Straight Line in a Regular Network?
Figure 7-23 is a net in a plane where all the points are arranged in a square formation. The net consists of all the points in the XY plane that are whole numbers. Imagine each point in the net as representing a pole sticking vertically out of the plane. If you place yourself at the origin, O. and look out at the network of poles, you will see some of the poles, while others will be hidden behind a few of the poles that are closest to you. In the figure, the dots indicate only the poles that are visible from the origin at 0. The unmarked points at line crossings represent poles (points) that can not be seen from the origin, because they are behind the ones that can be seen. Every point, whether marked or unmarked, has a coordinate number. For example, the coordinates of the point where x=3, and y=2, is (3, 2), but we will identify the point as a fraction 2/3, which is y/x. The interesting feature of identifying each point by a fractional number is that every point that can be seen will have a fraction that can not be reduced to a smaller quantity; for example, for the point at (12, 10), we get a fraction

of 10/12, which can be reduced to 5/6 (therefore the point at (12, 10) is, not visible). The point at (6, 5) has a fraction of 5/6, which can not be reduced any more, so it is visible. In other words, each point that can not be seen has a fraction that can be reduced to a simpler form using whole numbers only.
Let us now consider the XY plane extended to infinity with a pole or point present at every whole number coordinate out to infinity. Can we tie a rope at the origin and extend it in a straight line out to infinity so that it never touches any other pole? The answer is yes--there is ar infinite number of lines or ropes that could be tied to the origin and stretched out to infinity without touching another pole. In fact, there are infinitely more lines that can be drawn that don't touch a pole, than the number of lines that actually touch a pole or point. As a result, if you were to draw a random line in any direction through the lattice, the chance of hitting a point is practically nil. This last statement is true if each point is considered to be infinitely small, and each line infinitely thin. In Figure 7-23 the lines are about 4/10 of a millimeter, and the dots are roughly 1 and 1/2 millimeters in diameter.
The network of points in Figure 7-23 is also symmetric in every direction, if the origin from which we look out is placed at the center of any square. In fact, the network is symmetrical in all directions, regardless of where we put the origin. Let us place the origin at random, in any position in between any actual line crossing shown in the figure; looking out from this random origin, we will find a completely different group of points blacked out than if we placed ourselves at one of the regular points of the net. The significant feature is that when we have a symmetrical arrangement of points in space, the points will look symmetrical from any position we may choose, inside or outside the network. The main difference is that the symmetrical pattern will look different from differing positions; but the simplest and most regular symmetry patterns will occur when we use preferred positions like the origin.
Symmetry and Equilibrium
Any situation in the real world is called chaotic when we are in complete ignorance of what is really happening. Any seemingly random or disorderly activity in nature becomes very reasonable and orderly once we understand all the processes involved. The movement of every living and non living thing in a city, a country, or for that matter the Universe, can be accounted for, every second of the day. It is incontestable, that every movement of any storm center or high pressure center on the Earth's surface must be exactly counterbalanced by a very orderly movement of an air mass somewhere else on the globe. There is no such thing as random spacing of highs and lows over the surface of the Earth. Every vortex takes into account what every other vortex on the Earth is doing, before making its own move.
Looking at the examples in the chapters with the charts, it almost seems as if the vortexes are in communication with each other-as if they were living entities.
When we look at a weather map of a certain fixed date and time, we can see the instantaneous position of every vortex on the map as it appeared on the Earth. If a vortex decides to change size or direction for some inner reason of its own, a certain amount of time must elapse before this "decision" can be communicated to every other vortex (at the speed of sound). This is in accordance with Albert Einstein
emphasizing that events or occurrences between entities are not simultaneous because a certain amount of time must elapse before events can interact with each other.
Every entity in the Universe, when reacting to surrounding entities, tries to reach the "position of equilibrium" or symmetry, which is the simplest arrangement in nature. When outside energy is injected into a system, the entities that were in equilibrium will be forced out into asymmetric (nonsymmetric} patterns, and then attempt to swing back again into a symmetric or equilibrious pattern.
There can be what seems to be a "static equilibrium" of a ball resting on the surface of the Earth; or there can be "dynamic equilibrium" of a ball being supported continuously in the air by a high pressure stream of air; or there can be the "simulated equilibrium" of a living cell, which is seldom in equilibrium, since it is continuously absorbing and expending energy.
In the real world, patterns are always oscillating from a position of equilibrium to a position of increasing asymmetry (say positive) on one side, and then back through the equilibrium position, to a position of increasing asymmetry (say negative) on the other side. The symmetric equilibrium position occurs only for a fleeting instant. Any object subjected to varying outside forces will be in an asymmetric phase most of the time. Nevertheless, the asymmetric phase is just as orderly as the symmetric or equilibrium position, but it just doesn't look as neat. The asymmetric position can, of course, be broken down into a group of completely symmetric smaller units. There is no true chaos. When someone states that a situation is chaotic, it is only an admission of ignorance as to what is happening.
The comments of Gilbert Chesterton in Orthodoxy are appropriate at this time:
"The real trouble with this world of ours, is not that it is
an unreasonable world, nor even that it is a reasonable one.
The commonest kind of trouble is that it is nearly reasonable,
but not quite.... It looks just a little more mathematical and
regular than it is; its exactitude is obvious, but its inexactitude
is hidden; its wildness lies in wait."
As an example, Chesteron has an extraterrestrial examine a human body for the first time. He sees that the right side exactly duplicates
the left with two arms, two legs, two ears, two eyes, two nostrils, and two lobes of the brain. Going a little further, he finds a heart on the left side. He brilliantly calculates that there is another heart on the right side. Unfortunately, he stumbled over that one.
"It is this silent swerving from accuracy by an inch, that is
the uncanny element in everything. It seems a sort of secret
treason in the Universe . . . Everywhere in things there is this
element of the quiet and incalculable."
Close examination of crystals in the mineral world, and of real honeycombs in the world of bees, shows that they are not accurately regular, geometrically speaking. When the deviations from regularity is small in a crystal, there will still be a high degree of geometric order. It is considered as a crystal with defects. These small defects, however, highlight the importance of understanding imperfection. These defects are common in the crystalline world; they play a critical role in the actual formation of the crystal; and they affect the resulting physical properties of the crystal. Similarly, defects that occur in the symmetry of weather patterns, are signals of change.