General

We put the camel's nose under the tent when we discussed wavenumber. We may as well put the whole camel into the tent and touch on a few of the well established features of waves.

The variety of wave phenomena observed in nature is immense, yet there are many features common to all kinds of waves. There are sound waves, water waves, radio waves, seismic waves, gravity waves, Rossby weather waves, etc. Any explanation of "how the weather works" on a global basis would inevitably have to involve wave phenomena. There are shelves of books that deal with only one small part of the wave complexities. All we will do is to define a few of the basic wave phenomena and how waves interact with one another. This information is provided for those readers who are not familiar with this subject.

The Universe is full of things that move. These movements can be broken down into two broad types depending on whether the thing that moves stays near one place or travels from one place to another. Examples of things that stay near one place are a vibrating violin string, a swinging pendulum, water sloshing back and forth in a bathtub, and the electrons oscillating around an atom. Examples of things that move from one place to another are ocean waves moving towards a beach, the electron rays of a television tube, a light ray from a star reaching your eye. In some cases, both types of movement can occur simultaneously. The ocean waves may be traveling towards the beach, but a ball on the water's surface will only go up and down and forward and backward without traveling to the beach. You can make a wave travel along a stretched rope from one end to the other; the rope

58

itself vibrates up and down but does not move from its points of attachment.

Equilibrium

Usually, every material object can find at least one position in which it can remain at rest. This position is called a position of equilibrium. Any small outside disturbance (such as a push, pull, knock, etc.) will make the body move out of the equilibrium position to a new position. When that happens, the forces on the body are no longer evenly balanced and the body experiences a restoring force which tends to pull it back to its original position. This restoring force starts by dragging the body back toward its original equilibrium position. In time it reaches this position, but since it is moving with a certain amount of speed, it overshoots the position and travels a certain distance on the other side before stopping. Now it experiences a new force tending to pull it back; again it gives in to this force, picks up speed, overshoots the equilibrium position, and so on, until it stops due to friction or other forces. This kind of motion is called an oscillation. When a body moves a very small distance, the motion is called a vibration. This type of vibratory or oscillatory motion is defined as simple harmonic motion.

At this point, I might add that there are certain boundaries or limits to the equilibrium position. A pendulum can be made to swing in larger and larger arcs, always passing through the same center of equilibrium, each trip. A strong enough push, however, will break it completely off its pivot point and force the pendulum to fly off in one direction. This would set up new limits for the equilibrium position of the pendulum; like lying on the floor.

Oscillations and Resonance

A free or natural oscillation occurs when something is given an initial movement by an external force, and is permitted to oscillate freely without any additional outside force being added after the first push (like the first push of a swing). A body may be kept in motion by regular or periodic impulses delivered by an outside force. In that case, the body is said to be executing forced oscillations. When the frequency (determined by the properties of the oscillating object) of the forced oscillation is the same as the natural frequency of the oscillating body,

59

the natural oscillations will reinforce the outside forced oscillation. The amplitude is the maximum distance that an oscillating body moves away from the equilibrium position. The amplitude of the forced oscillation increases as the period of the oscillation approaches that of the oscillating system and becomes very large when the two periods coincide. When this occurs, we have a condition which is known as resonance. When the forced oscillation has a different frequency from the free oscillation of the body, the received impulses sometimes help and sometimes interfere with the natural oscillations.

Harmonic Movement

It has been shown that the motion of a complicated system having many moving parts can always be considered as being made up of simpler movements, which are called modes of operation, all going on at the same time. If a complicated system has a large number of modes we find that each one of its modes still is acting as if it were independent with each individual mode retaining its own properties that are similar to a simple harmonic oscillator.

We can consider that a circular motion performed at a constant speed can be regarded as being made up of two simple harmonic motions in directions at right angles to each other. In Figure 6-1, point P moves around circle XYX' Y' with constant speed, like the hand of a clock. At any given position of P. draw a perpendicular PN on to the line XX', and a perpendicular PM on to the line YY'. Then as P goes around the circle, N moves back and forth along line XX', at the same time M moves up and down line YY'. Each one of these two points is executing simple harmonic motion.

It is sometimes convenient to think of the harmonic movement of a point at a uniform velocity around a circle as a sine wave. See Figure 6-2. As P moves around the circle it creates a harmonic sine wave

60

(which is shown by the waveform to the right of the circle in the figure) as a function of time. Theta, which is called the phase angle, is the angle PON, in Figure 6-2. This angle changes continuously as P goes around the circle. When point P starts out at position N. the angle for theta is zero and the time is zero. When point P reaches the position labeled P. the angle is 45°. Since it took some time for the point to reach position P from N. we can consider the size of angle theta as a measure of time; therefore we mark off the X-axis or time axis in degrees. At 45°, point P is a certain distance above the X-axis, and a certain distance from the Y-axis (which lies along OQ); so we draw dashed lines from P to P'and from 45° on the X-axis to P' (which is the point where the two dashed lines cross). The same procedure is followed to locate the points Q', R', S', T', U', V', and N', to generate the sine waveform, which is a harmonic wave since it is generated by harmonic motion, as defined in Figure 6-1.

Fourier Analysis

Anything that repeats itself after a fixed amount of time is called a periodic time function. In a periodic wave, one pulse follows another in regular succession. Sound waves, water waves, and light waves are almost always periodic, although in each case a different quantity varies as the wave passes. In general, periodic time functions are not simple waves, but are quite complex. It was shown by J. B. Fourier (1768-1830) that any complex periodic time function can be accurately described as the sum of a series of harmonically related waves.

The procedure of breaking up a given periodic wave into simple harmonic components and determining the equation and/or the harmonic waves which represents it, is called Fourier analysis or

61

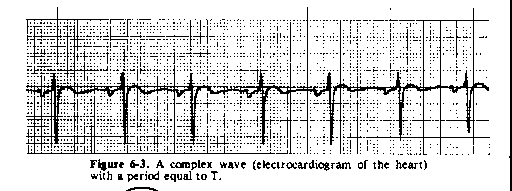
harmonic analysis. Fourier stated that every curve (wave), no matter what its nature may be, or how it was developed, can be faithfully reproduced by superimposing a sufficient number of simple harmonic curves (waves). Figure 6-3 is an example of a complex periodic wave with a period of T.

62

The components necessary to construct one type of complex wave (of which there are an infinite variety) is shown in Figure 6-4. The fundamental wave (or simple fundamental) of a group of waves with different frequencies is that wave with a frequency that is the lowest common denominator of all the other frequencies. Since the fundamental is the first harmonic, then the second harmonic is a wave that has twice the frequency of the first harmonic. The third harmonic has three times the frequency of the first harmonic, and so on for the fourth, fifth, etc., harmonic.

Wave Pulses

Wave motion can be considered as the transport of energy and momentum from one point in space to another point without the actual transport of matter. In water waves, waves on a rope, or sound waves, the energy and momentum are transported by a disturbance in the medium, which is carried forward because the medium has elastic properties. When a rope is stretched and put under tension and then given a small shake at one end, we find that the string will change shape in a regular manner as shown by Figure 65. The wave pulse moves to the right; the change in shape of the pulse as it moves along is called dispersion.

Interference

Interference occurs when two waves meet and combine to form a resultant wave. The fact that two or more waves add algebraically is called the principle of superposition. In Figure 6-6a, we see a crosssection showing the crossing of a larger and a smaller wave with

63

constructive interference which gives a resultant wave that is greater than any of the original waves. In Figure 6-6b, we see the crossing of two waves that are similar in size but are opposite in phase (angle), which causes destructive interference due to the cancellation of pulses.

When waves are in a confined space, like when we pluck a string whose ends are fixed in place, or in an organ pipe, we will find that reflections bounce off both ends. Therefore, we will have waves traveling in both directions. These waves will add in accordance with the principle of superposition when there is interference. For each string or pipe, there are always certain frequencies where the interference, created by vibrations, causes a stationary pattern which is called a standing wave. Figure 6-7 shows standing waves on a rope that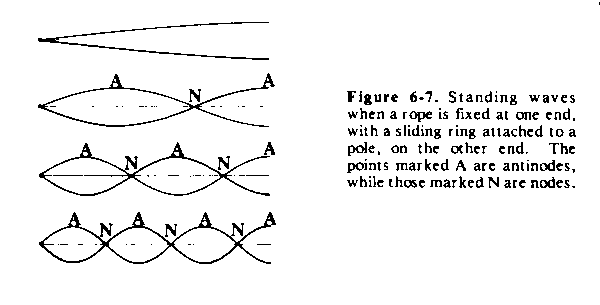

64

is fixed at one end and is attached to a ring at the other end which is free to slide up and down along a pole. The points marked A, are antipodes, where the displacement of the rope varies between its widest limits.

The points marked N. are points of zero displacement where the rope does not move at all.

Up to now we have been considering only the type of waveforms that repeat themselves indefinitely or wave forms that occur only once. There is another type of wave that changes with time, which goes on indefinitely, but does not repeat itself periodically. Such waves (or functions), being relatively unpredictable, are called random time functions. Traffic noise, the babble of conversation in an auditorium, the noise of construction etc., are all random time functions, since one never knows exactly what the next sound will be.

The spacing of all vortexes and other significant features such as troughs and ridges on a weather map over an entire hemisphere have been falsely considered, by meteorologists, to be of a random nature. Therefore, it is the main purpose of this text to prove that the positioning of vortexes is not random, but is beautifully organized.

65