
Chapter 4
Organization in Space
Space and Some of its Features
In chapters 13 and 14, I show some aspects of an orderly arrangement over a hemisphere of low pressure centers, high pressure centers, and cols (which are points between pressure centers). Therefore, it is appropriate at this time to investigate the subdivisions of space and the mathematical explanation of spatial order. This question of spatial order, or space patterns, is of great importance whether we look at the arrangement of particles in the nucleus, the arrangement of molecules in chemicals, the spiraling of planets, the whirling of galaxies, and, oh yes, the "dance" of highs and lows over any planet with an atmosphere. Space may be an empty nothing, but it does impose irresistible controls over all bodies that dwell in it. These restraints don't depend on any specific types of forces; they are only determined by geometrical rules.
The first explanation of space started with the Pythagoreans (548 B.C. to 490 B.C.). They looked for patterns that could be repeated over and over again on the surface of a plane, and that would fill in that plane completely (like tiles on a floor). They came up with the only regular polygons that could be used for this purpose. Note that a regular polygon is a three, or more, sided figure which has equal sides and equal angles. They found that there were only three regular polygons which would fill in a plane; an equilateral triangle, a square, and a regular hexagon. See Figure 4-1,below. Nevertheless, there are an infinite number of irregular polygons that can provide this kind of tiling-a triangle of any shape or any four sided figure will also fill in a plane.
The three dimensional analog, or resemblance, to a regular polygon is
a regular solid. Before we proceed we will add a few definitions so that
we don't get lost in the terminology. A polyhedron is a figure or
solid
formed by many plane faces. Polyhedrons are named in accordance with
the number of plane faces they have. Therefore, polyhedrons of four, five,
six, etc., faces are called tetrahedron, pentahedron, hexahedron, etc.,
respectively. 
Figure 4-1. The triangle, the square, and the hexagon are the only regular polygons that will fill a plane completely.
If all the faces of a polyhedron are congruent (identical), the solid is called a regular solid or regular polyhedron. There are only five regular solids possible as shown in Figure 4-2.

The Egyptians discovered the first three regular solids: the regular tetrahedron, which has four faces, each face an equilateral triangle, with three faces touching at each vertex; the regular hexahedron or cube, which has six faces, each face a square, with three faces at each vertex; and the regular octahedron, which has eight faces, each one an equilateral triangle, with four faces at each vertex. The Pythagoreans discovered the other two: the regular dodecahedron, which has twelve faces, each a regular pentagon, with three faces at each vertex; and the regular icosahedron, which has twenty faces, each an equilateral triangle, with five faces at each vertex.
A pattern for making each of the five solids may be formed of cardboard by drawing and cutting out the figures shown by solid lines in Figure 43. All you have to do is fold along the dotted lines and tape the free edges together.
Later on we will be looking at the angular relationships between highs and lows on the polar stereographic map. To cast some light on

why these relationships exist, we will take a closer look at the regular
solids and see why only five are possible. First, we must prove that the
sum of the face angles that meet at a vertex of a polyhedron must always
be less than 360°. To understand why this is so, take a flat piece
of paper (crumpled paper doesn't work very well) and mark a point in approximately
the center of the paper. Label this point P. Now draw 7 lines of equal
radius out from point P; join the ends as shown in Figure 4-4a. You will
end up with a group of 7 angles adding up to 360°. Now cut out this
7 sided figure (septagon) and crease along each line. Try to form
a polygon by folding along the creases. You'll find that you can't make
polyhedral angles whose edges are along the creases. The angles will not
fold out of the plane of the paper unless the paper kinks. Now cut out
one of the angles, for example, the one whose sides are PA and PG in Figure
4-4b; then bring PA and PG together and tape it to make a polyhedral angle.
This shows that the sum of the face angles of a polyhedral 
angle must always be less than 360° . To turn a flat piece of paper into a three dimensional structure, you must always remove a triangular dart. Remember that a flat piece of paper has thickness, and so you are not really cutting out just a flat triangle, but actually a polyhedron.
For a polyhedral or three dimensional angle to exist, there has to be three or more faces meeting at a vertex. The regular polygon with the least number of sides is the equilateral triangle where every angle is 60°. Only three different polyhedral angles can be formed with only equilateral triangles meeting at the vertex. The first is the tetrahedron with three equilateral triangles at each vertex (Figure 4-2a), this give 3 times 60° or 180° around each vertex. The second is the octahedron with four equilateral triangles (Figure 4-2c), which gives 4 times 60° or 240° around each vertex. The third and last possible one is the icosahedron with five equilateral triangles (Figure 42e), which gives 5 times 60° or 300° around each vertex.
Each angle of a square has 90°. A cube consists of six squares, where there are three squares at each vertex. Therefore you have a polyhedral angle at each vertex equalling 270°. If you had four squares at each vertex, you would end up with 360°, in other words, a plane, and not a solid.
Each angle of a regular pentagon (a 5 sided figure) has 108°. A dodecahedron consists of 12 regular pentagons where there are 3 regular pentagons at each vertex. Therefore, you have a polyhedral angle at each vertex squalling 324°.
Each angle of a regular hexagon (a 6 sided figure) has 120°. Three such angles would add up to 360°, in other words, a plane. Therefore, a polyhedral angle can not be formed from regular hexagons-so, no regular polyhedron can be formed with hexagons.
The closer the sum of the angles around a vertex add up to 360°
(for any polyhedron, regular or otherwise), the closer we come to having
a flat surface, which is shown in Figure 4-5. The pointiest regular solid
is the tetrahedron with 180° at each vertex; on the other hand, the
flattest regular solid is the dodecahedron with 324° at each vertex.

There appears to be a contradiction here. The sum of the angles around
any vertex of a polygon is less than 360°, yet you can stand on the
vertex and spin around a complete 360°. This seeming paradox can be
resolved relatively easily if you consider a flat plane touching the vertex
point. The plane should be perpendicular to the most symmetric axis that
passes through the vertex. Now project all the edges of the polygon up
into the plane. Imagine yourself standing at the vertex in the plane and
looking down on the tetrahedron, you will see the 60° faces sloping
down. When you look at the projected edges on the plane, you will note
that each of the 3 angles is 120°, not 60° as on the polygon. See
Figure 4-6. 
Figure 4-6.
a. The angles at the vertex of a tetrahedron are actually 60°, but they project onto a plane as 120°. Since it is difficult to insert a real tetrahedron on this page, we must do with a flat projection which is drawn showing the angles of 120°. The shading on the drawing is what saves the day by indicating that we are looking at a perspective drawing of a tetrahedron.
b. The angles around the vertex of an octagon are also actually 60°, but project as angles of 90° in a plane.
You might ask, "What does all this have to do with the sphere of the Earth?" Well, the Earth is also a polyhedron, but a round one. The surface of a sphere can be considered as consisting of a very large number of vertexes; all joined to each other by straight lines or chords. If you stood at one of the vertexes and looked down, you would find the sum of the angles total to something slightly less than 360°. That the Earth is a polyhedron with an immense number of vertexes is not as strange as it may seem at first, since the Earth, in reality, consists of an immense number of electrons and protons at the atomic level with all of them separated by finite distances.
As a practical matter, let us consider a cluster of actual high and low pressure centers on the surface of the Earth which are separated by great or small distances. Every one of these highs and lows could be joined by straight lines or chords which would represent the chordal distance between their centers. These chords represent the shortest
distance, in absolute space, between two points and actually pass below the surface of the Earth. If you were at the center of one of these highs or lows, you would know that the sum of the angles around that vertex or center would be less than 360°.
This complication can be approached in two different ways. First, these highs and lows are drawn on a flat paper map. Then the chords between the highs and lows are projected onto the flat map. And so the sum of the angles around each high and low on the map now adds up to exactly 360°. The advantage of using a flat map of a round world is that it becomes possible to use straight lines in making certain types of calculations dealing with the surface of the Earth, or for that matter any other sphere. Anytime that you can use straight lines to show relationships on a sphere, you have gained a great simplification in the type of mathematics required. Secondly, the centers of highs and lows surrounding a given high or low could be joined by arcs drawn on the surface of the Earth. Any high or low could be considered as a pole with lines of longitude radiating outwards. Therefore, the sum of the angles around a vertex, using arc curves will add up to exactly 360° (in the same way that the longitude lines add up to 360° around the North pole) .
Let us explore some more of the conditions on the surface of a sphere that are not necessarily obvious. We will analyze the matter of dimensions or degrees of freedom. A point inside a cube can move in three mutually perpendicular independent directions (three degrees of freedom) at any given moment. Therefore, space inside a cube is three dimensional. But a point confined to the surface of a cube can move in only two degrees of freedom at any given moment. Likewise, the space inside a sphere is three dimensional, while the surface of a sphere, even though it is not flat, is twodimensional (only two degrees of freedom for a moving point at any given moment). On the surface of the Earth, these two degrees of freedom are described by latitude and longitude (which are curved arcs). The fact that the Earth is not a perfect sphere and that it has bumps on it such as mountains does not alter the fact that there can be only two degrees of freedom on a surface.
A tetrahedron can be placed inside a sphere so that all 4 vertexes will lie on the surface of the sphere. The same thing can be done with the 4 remaining regular solids, and of course each vertex will lie on the surface of the sphere. Note that a line joining any two adjacent
vertexes in a regular solid is always an edge of that solid. And so each edge of the regular solid that is inside the sphere becomes a chord of that sphere, since each vertex touches the surface of the sphere.
Let us now project the edges or chords of these regular solids onto
the surface of the sphere by using the center of the sphere as the point
of projection; this is shown in Figure 4-7. This procedure generates the
spherical tetrahedron which is known as the tetrahedral; the spherical
hexahedron, known as the hexahedral; the spherical octahedron, known as
an octahedral; the spherical icosahedron, known as an icosahedral; and
last but not least, the spherical dodecahedron, which is known as a dodecahedral.
The corner angles or polyhedrals in these spherical polyhedrons are
much larger than their flat faced friends due to their spherical excess.

All five of the regular polyhedrons plus some more complicated ones appear in various forms of life. Some examples are shown in Figure 4-8 and 4-9 that were mainly taken from Art Forms in Nature, by Ernst Haeckel (2).
Likewise, there are a huge variety of crystal forms of inorganic or nonliving matter that take the shape of three of the regular polyhedrons (tetrahedron, hexahedron, and the octahedron). The icosahedron and the dodecahedron do not occur in crystal form. It has been proven mathematically that these two forms can not occur due to the fact that crystals are built up from individual particles (atoms) or quantum units that can not be further subdivided in a crystal form. You would need some fractional parts of atoms to build an icosahedron or dodecahedron.
Space Filling Patterns on a TwoDimensional Surface
We will now take a more detailed look at space filling patterns, regular and irregular. These types of patterns have been called tiles,


lattices, and tessellations. Regular tessellations (the ones
discovered by the Pythagoreans) are those configurations made of regular
polygons of one kind only. These are the patterns of squares, triangles,
and hexagons that we have pictured in Figure 4-1. In semi-regular tessellations,
the pattern is the same at every vertex, but more than one type of polygon
appears in each configuration. It has been proven that there are only 8
of these types possible; these are shown in Figures 4-10 below. Thus, in
4-lOa, there are 2 triangles and 2 hexagons at each vertex; in 4-lOb, there
are 4 triangles and 1 hexagon at each vertex; etc. In demi-regular tessellations,
we still use regular polygons, but the pattern in which they are used
is different for different vertexes. 


Go to page 39 for the remaining demi-regular patterns.

It is also possible for the vertexes of some polygons to lie on the
sides of other polygons to form other tessellations which can be seen in
Figure 4-12. 
Figure 4-12. Vertexes of these polygons lie on the sides of other polygons.
There are some additional figures that can fill a plane with no gaps
or overlaps when they undergo parallel translations. These are the parallelogons.
They are squares or regular hexagons or configurations that are derived
from them by elongations or compressions. See Figure 4-13 below. 
Figure 4-14 on page 41 is a more detailed version of Figure 4-13. Lines of symmetry divide each shape (in figure 4-14) into parts which are similar to one another. There are four kinds of lines of symmetry:
We can draw similar irregular patterns on a surface weather map if we replace all the high and low centers with points and join the points with straight lines.

Figure 4-14. Some differing combinations possible with a square and hexagon, subject to compression or elongation. The lines that are drawn inside these figures represent lines of symmetry or reflection.
Principles of Closest Packing of Spheres
The investigations of filling space in a plane with geometric figures eventually led to the investigation of the closest packing of spherical objects in threedimensions. Understanding the principles of closest packing of spheres led to immense discoveries in many fields of science. In nuclear science it led to a detailed explanation of how the electrons and protons are packed in all the elements of the periodic table. In the field of biology, it led to a better understanding of how cells are related to each other; why various forms of life assume their shapes and forms;
why the honeycomb of a bee is made of hexagonal cells; etc. In physics and chemistry, it has led to an insight into the structure of soap bubbles; foaming of chemicals; etc. There has yet to be a peep on this subject in the field of weather analysis and forecasting. Dear reader, let us now rectify this situation and bring (drag if necessary) meteorology out of the dark ages and into the stream of modern science.
We will now focus on the two dimensional aspect of closest packing of spheres, since the spacing of highs and lows over the surface of the Earth is a two dimensional phenomenon. We will also study some of the aspects of three dimensional packing to aid us in the evaluation of the two dimensional variety of closest packing of spheres.
Spheres of the same size can be piled and packed together in many different
ways. If we arrange the spheres or circles in a triangular formation, the
number of circles involved will be a triangular number. If we make a square
formation, the number of circles will amount to a square number. See Figure
4-15. 
The Pythagoreans were the first to link numbers and shape. They reasoned that the numbers 1, 3, 6, 10, etc., (gotten by taking the sums of 1, 1+2, 1+2+3, 1+2+3+4, etc.), are triangular numbers; while the numbers 1, 4, 9,16, etc. (gotten by taking the products of 1 x1, 2x2, 3 x 3, 4 x4, etc.), are square numbers. These are the simplest examples of what the "old timers" called figurate numbers. A famous book was written by Blaise Pascal, explaining figurate numbers, and although little attention is given them today, they still provide intuitive insights
into many aspects of elementary number theory and geometry. In the measurement
of lengths, areas, or volumes, numbers are intimately related to space.
In this manner, we find that geometry, which is a study of space, is fused
with arithmetic and algebra, which are the study of numbers. We usually
think of numbers as being lined up in a straight line with numbers related
to each other by a simple relationship such as: larger than or smaller
than. Here we consider numbers as two dimensional (or three dimensional
when appropriate) entities with each number acting as a part of a geometric
structure. In a geometric sense, all vortexes or other points of interest
on a weather map could be considered as a structure of geometric numbers.
Figure 4-16 below shows an 
arrangement of polygonal arrays of points having 1, 2, or any number of points radiating out from the lower left hand corner. We can count the points in the pentagon of Figure 4-16c, in a similar manner as was done in Figure 4-15, to make the pentagonal series of 1, 5, 12, 22, 35, etc., points. Likewise, in Figure 4-16d we have the hexagonal series of 1, 6, 15, 28, 45, etc., points. We have been using the terms, points and circles (and spheres also), interchangeably, and it should not be confusing if we consider a point as a very small circle.
The figurate numbers are related to each other in various ways. For
example, Figure 4-17 shows the fundamental connection of the square with
triangular figurate numbers.  Figure 4-18 on page 44 shows the figurate series when the starting number
is a nuclear sphere in the center
Figure 4-18 on page 44 shows the figurate series when the starting number
is a nuclear sphere in the center

instead of a corner as in Figure 4-16. In this case the series runs 1, 7, 19, 37, etc.
We will now explore another feature of space-filling that was first
recognized by Leonhard Euler (1707-1783) (3)-that no system of hexagons
can enclose space no matter if the hexagons are equal or unequal,
regular or irregular. Euler showed that a pattern of hexagons may be extended
as far as desired over a plane or curved surface as long as it never closes
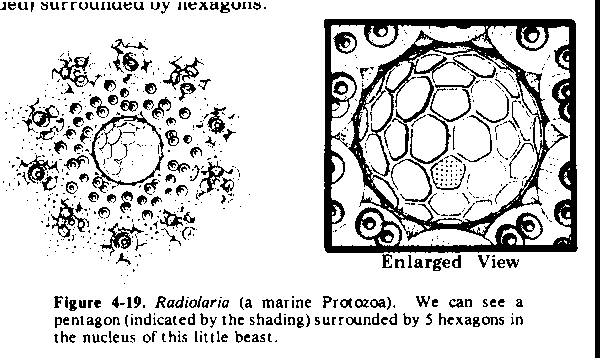
in. On the other hand, 5 hexagons can be arranged around a nuclear pentagon,
on the surface of a sphere. An example taken from real life, shown in Figure
4-19, where we see a pentagon (which I have shaded) surrounded by hexagons.
Examples and Experiments in Closest Packing of Spheres
We start with four spheres that can come in contact with each other in one of two ways: either as a square formation (Figure 420a) or as a

nested formation (Figure 4-20b). The square formation is unstable and
tends to slide into the nested pattern which is the stable one. In embryology,
it has been found that a segmenting egg, with 4 or more segments, will
take a shape, where only 3 cells are in contact at a vertex-which is the
nesting position. The 3 cells meet at angles of 120°. In the example
of Figure 4-21, we see that an individual cell 
(made of soft material) that would be spherical by itself, forms a flat
line of contact with an adjoining spherical cell that presses against it.
Conklin (4) in 1897 called the line which joins the two vertexes of triple
contact, the polar furrow. We see a similar geometric pattern on
the skeleton of the Dictyocha stapedia in Figure 4-22. 
In 1727, Stephen Hales, an English physiologist wrote about an experiment where he poured peas into a pot to find the closest packing arrangement possible using equal sized spherical objects. The experiment has been repeated many times since in many different forms. The two dimensional view for closest packing of equal sized spheres is shown in Figure 4-23, where we start with a sphere in the center. It is a simple geometrical fact that each of the equal sized circles

is in contact with six others around it. Each circle has 6 points of contact with 6 other circles. Imagine if you will, that a whole system of circular bodies are under a uniform stress of pressure by growth or expansion inside the cellular circles. The 6 points of contact will now become 6 lines of contact between the circles. The equal circular bodies will be converted into equal hexagons, where the angles at the vertexes are 120°.
This hexagonal symmetry of close packing is everywhere you turn. Bees
use this method for packing their honey in hexagonal bee cells to form
the honeycomb. Each bee busily fills up its cell until the sides of its
domain squeeze up against the cells of the 6 other bees surrounding it.
See Figure 4-24. In the third century, Pappus noted that by building
hexagonal cells in their honeycombs, the bees made a structure that stores
the maximum amount of honey with the minimum use of wax. 
Similarly, Ste'phane Leduc (5) conducted diffusion experiments with different chemicals and liquids to form "artificial tissues" of hexagonal shape, as shown in Figure 4-25. All biologists know that these patterns simulate the patterns in organic living tissues. As is well known, these hexagonal patterns also form in various combinations in snow flakes. So now we find these 120° equilateral angles of hexagons in both inorganic and organic arrangements of matter in space.
Another example can be shown with soap bubbles. The solid with the

greatest volume for a given surface area is the sphere. The soap bubble
encloses a fixed amount of air which is forced by the tension in the soap
film to take the shape that redistributes the enclosed air so that the
outside surface of the bubble is as small as possible. This makes the bubble
as close as possible to a sphere. Bubbles also collect in the manner of
closest packed spheres. Only the outer surface of the outermost bubbles
in a cluster of foam retains the spherical surface. Inside a bubble cluster,
all the bubble pressures become approximately equal; the points of contact
of the individual soap bubbles become lines or plane surfaces of contact
to form the familiar hexagonal shapes. See Figure 4-26. 
In 1900, H. Benard (6) reported on his experiments with cellular vortexes in a thin layer of liquid, warmed in a copper dish. Little vortexes or cells were formed as he heated the liquid. Whether he started with the liquid in motion or at rest, the geometric patterns formed, would ultimately become uniform and symmetrical. Before a condition of equilibrium was reached, he found mainly hexagonal formations, but 4, 5, or 7 sided cells were also present. The larger cells would tend to grow smaller, while the smaller ones would grow larger or disappear. When 4 cells met in a single corner, they would shift until only 3 cells met in the corner as required for the nesting formation. The sides of the cells would eventually adjust themselves to equal lengths and all the angles would become equal. Lastly all the cells would end up
with a fixed or quanta hexagonal size.
The experiment by Benard was actually preceded by E. Weber (7) and
has since been demonstrated many times in the laboratory. Weber showed
that when a layer of metallic paint mixed with solvent is placed in a dish
and allowed to evaporate, a regular pattern of convective motion will start.
This is caused by the cooling of the liquid on the top surface by the evaporation
of the solvent. This convection causes hexagonal shapes to form when a
steady state is reached, as is shown in Figure 4-27. The diameter of the
hexagonal cells is approximately 3 times their depth; varying the depth
of the liquid will vary the diameter of the hexagons. 
Angles of the Hexagon
It is obvious from all of the preceding information that the hexagon is spread throughout the Universe. Let us take another look at a few of the simple mathematical features of the hexagon. Figure 4-28a shows three equal hexagons meeting at point H. We would suspect the presence of hexagonal formations wherever 120° angles occur in any natural phenomenon. Figure 4-28b shows that a hexagon is really constructed of 6 equilateral triangles and that a circle can be circumscribed around a hexagon. Any radius, OA, OB, etc., is equal to the length of any chord, such as AB, BC, etc. The circumference of the circle is exactly divided into 6 parts by the 6 chords. All the angles in an equilateral triangle are 60°; therefore, it should be no surprise to see 60° angles occuring in any natural phenomenon that is infested with hexagons.
Euler said that all geometric patterns consist of three fundamental elements: lines (or trajectories), vertexes (or crossings), and areas (or openings). The triangle is the polygon with the minimum of sides that can enclose an area; which makes it the the fundamental quanta or
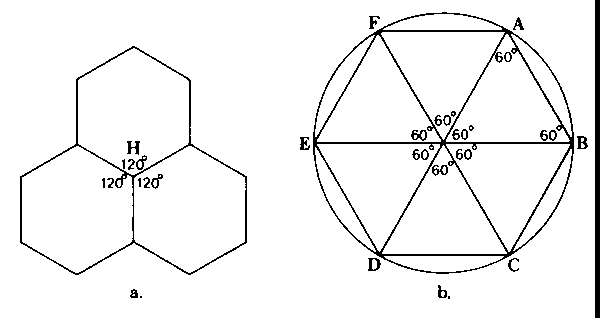
Figure 4-28.
building block for enclosing area. Even a square is built up by adding two triangles. With energy being injected into a system, as in Benard's experiment, we find that the average probability is a network of equilateral triangles that cluster in the form of hexagons.
In closing this chapter, it is not unreasonable to say that there is a large amount of statistical evidence (from other fields of science) that indicates there should be some types of similar geometric "weather beasts" in weather patterns.