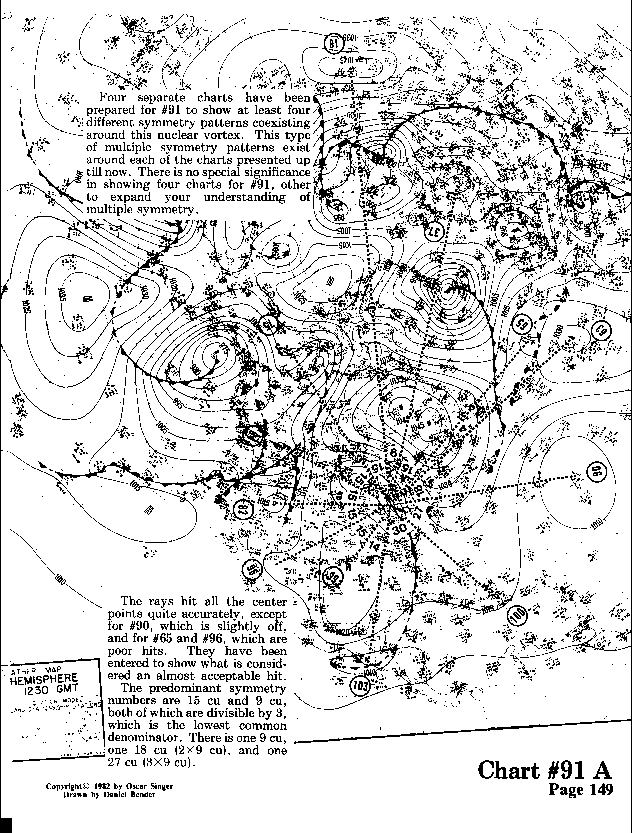
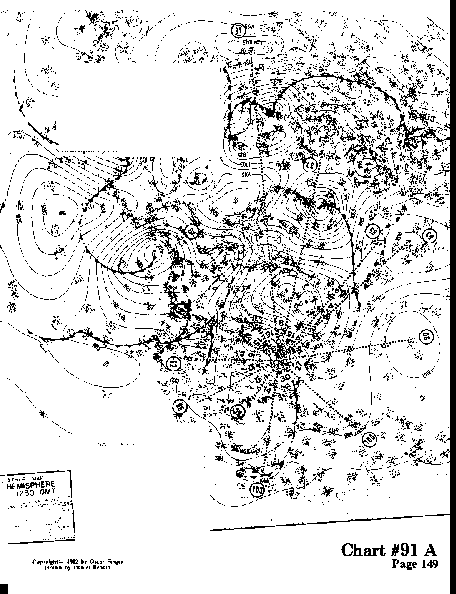
Four separate charts have been prepared for #91 to show at least four different symmetry patterns coexisting around this nuclear vortex. This type of multiple symmetry patterns exist around each of the charts presented until now. There is no special significance in showing four charts for #91, other than to expand your understanding of multiple symmetry.

The rays hit all the center points quite accurately, except for #90, which is slightly off, and for #65 and #96, which are poor hits. They have been entered to show what is considered an almost acceptable hit.

The predominant symmetry numbers are 15 cu and 9 cu, both of which are divisible by 3, which is the lowest common denominator. There is one 9 cu, one 18 cu (2x9 cu), and one 27 cu (3x9 cu).

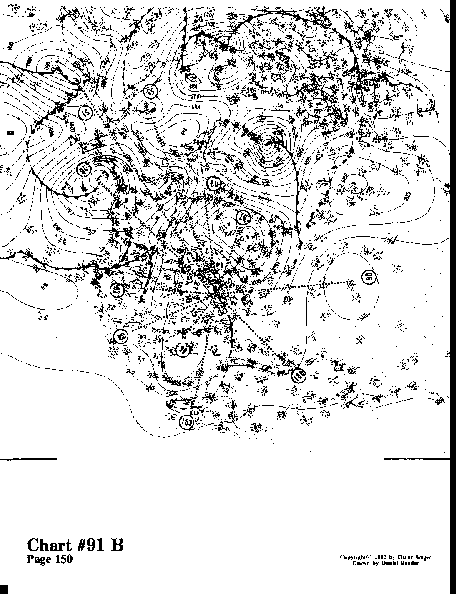
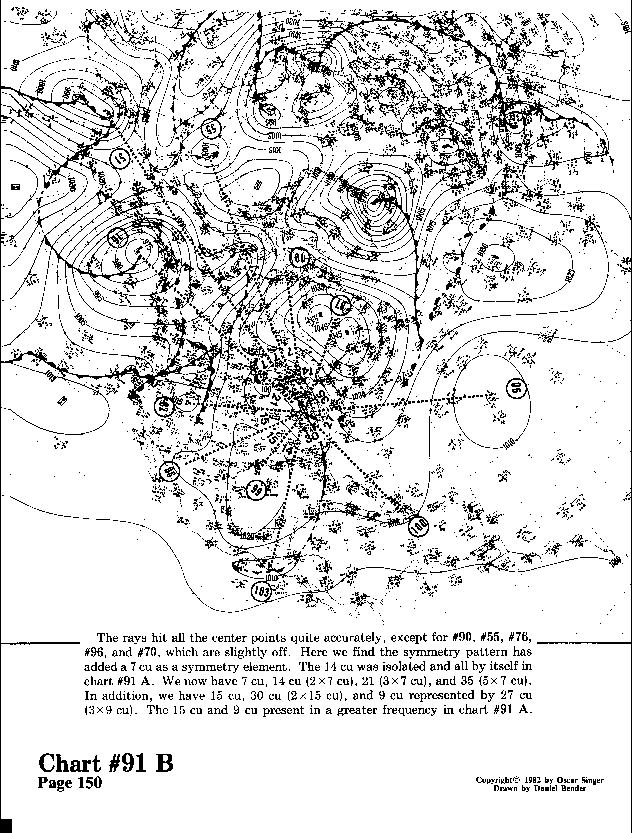
The rays hit all the center points quite accurately, except for #90, #55, #76, #96, and #70, which are slightly off. Here we find the symmetry pattern has added a 7 cu as a symmetry element. The 14 cu was isolated and all by itself in chart #91 A. We now have 7 cu, 14 cu (2x7 cu), 21 (3x7 cu), and 35 (5x7 cu). In addition, we have 15 cu, 30 cu (2x15 cu), and 9 cu represented by 27 cu (3x9 cu). The 15 cu and 9 cu present in a greater frequency in chart #91 A.

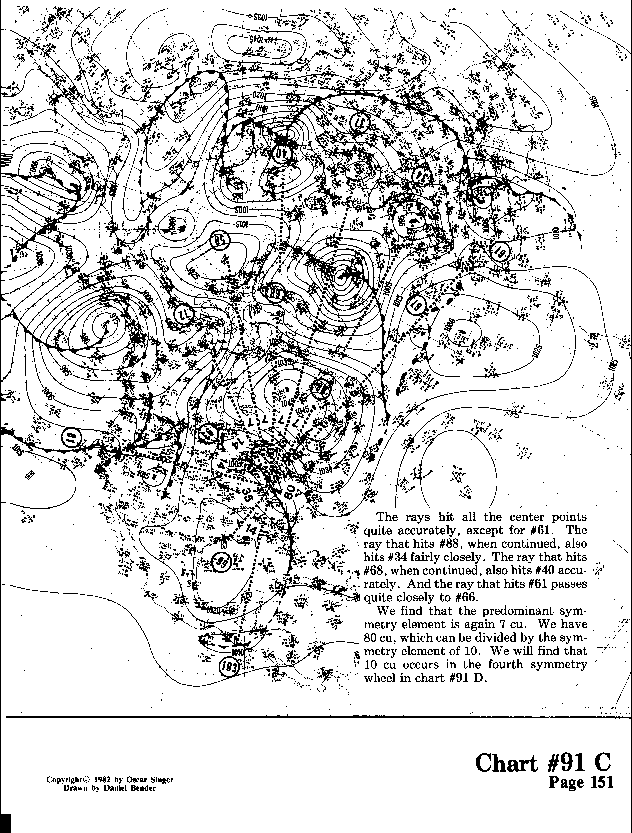
The rays hit all the center points quite accurately, except for #61. The ray that hits #88, when continued, also hits #34 fairly closely. The ray that hits #68, when continued, also hits #40 accurately. And the ray that hits #61 passes quite closely to #66.

We find that the predominant symmetry element is again 7 cu. We have 80 cu, which can be divided by the symmetry element of 10. We will find that 10 cu occurs in the fourth symmetry wheel in chart #91D.

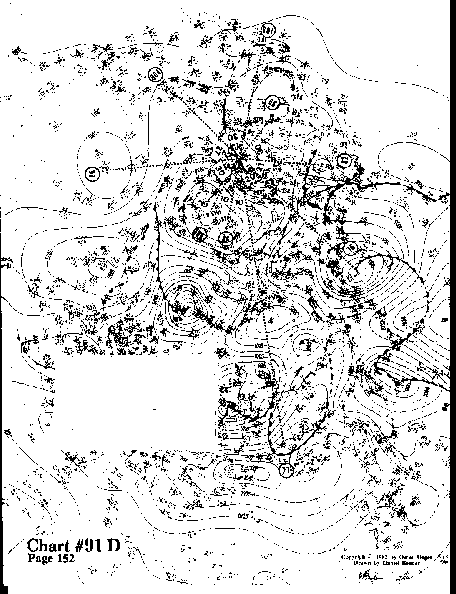
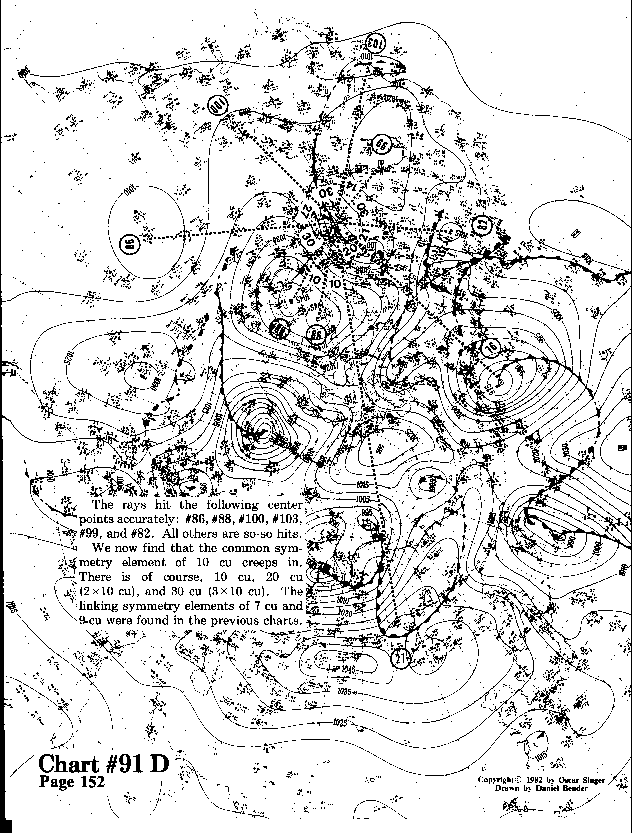
The rays hit the following center points accurately: #86, #88, #100, #103, #99, and #82. All others are so-so hits.

We now find that the common symmetry element of 10 cu creeps in. There is of course, 10 cu, 20 cu (2xl0 cu), and 30 cu (3xl0 cu). The linking symmetry elements of 7 cu and 9 cu were found in the previous charts.

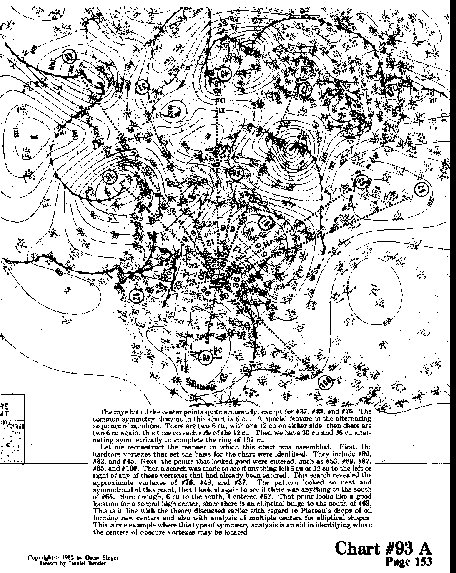
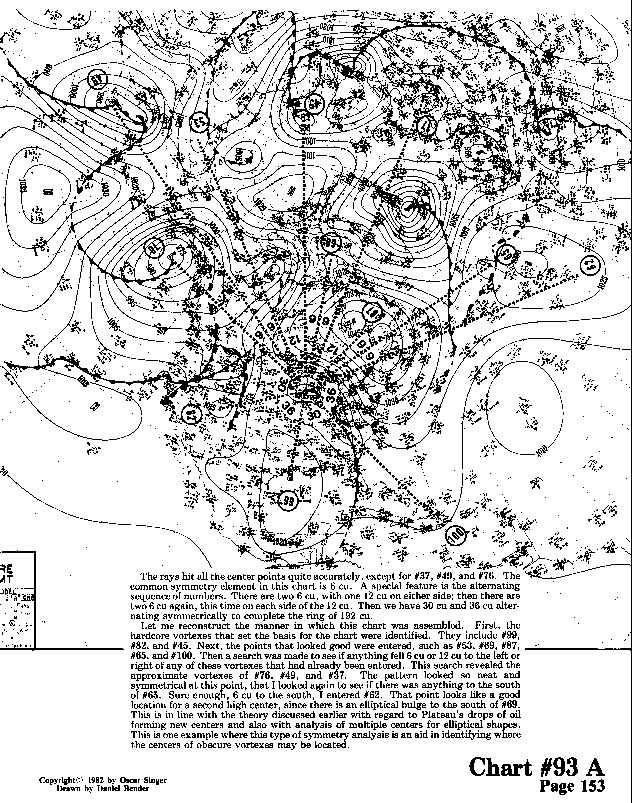
The rays hit all the center points quite accurately, except for #37, #49, and #76. The common symmetry element in this chart is 6 cu. A special feature is the alternating sequence of numbers. There are two 6 cu, with one 12 cu on either side, then there are two 6 cu again, this time on each side of the 12 cu. Then we have 30 cu and 36 cu alternating symmetrically to complete the ring of 192 cu.

Let me reconstruct the manner in which this chart was assembled. First, the hardcore vortexes that set the basis for the chart were identified. They include #99, #82, and #45. Next, the points that looked good were entered, such as #53, #69, #87, #65, and #100. Then a search was made to see if anything fell 6 cu or 12 cu to the left or right of any of these vortexes that had already been entered. This search revealed the approximate vortexes of #76, #49, and #37. The pattern looked so neat and symmetrical at this point, that I looked again to see if there was anything to the south of #65. Sure enough, 6 cu to the south, I entered #62. That point looks like a good location for a second high center, since there is an elliptical bulge to the south of #69. This is in line with the earlier discussion of Plateau's drops of oil that form new centers and also with the analysis of multiple centers for elliptical shapes. This is one example where this type of symmetry analysis is an aid in identifying where the centers of obscure vortexes may be located.

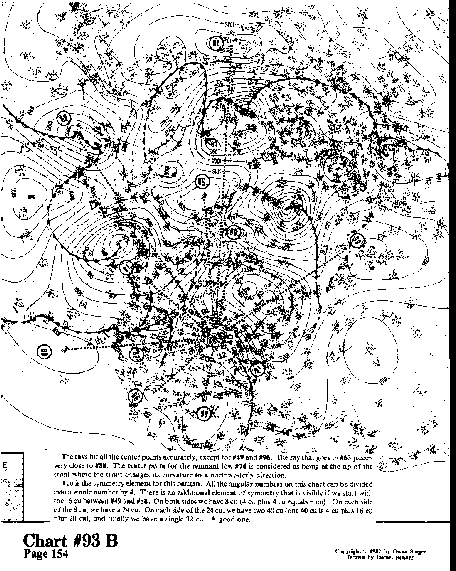
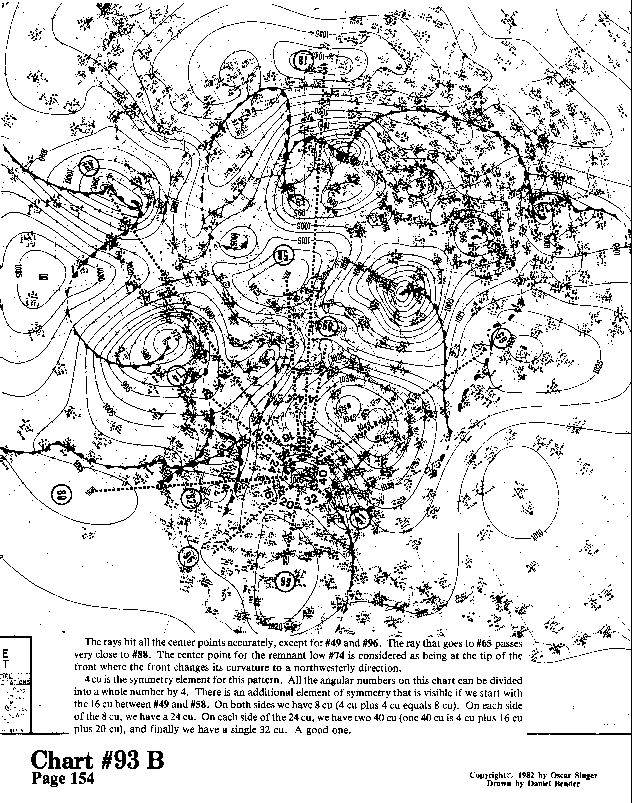
The rays hit all the center points accurately, except for #49 and #96. The ray that goes to #65 passes very close to #88. The center point for the remnant low #74 is considered as being at the tip of the front where the front changes its curvature to a northwesterly direction.

4 cu is the symmetry element for this pattern. All the angular numbers on this chart can be divided into a whole number by 4. There is an additional element of symmetry that is visible if we start with the 16 cu between #49 and #58. On both sides we have 8 cu (4 cu plus 4 cu equals 8 cu). On each side of the 8 cu, we have a 24 cu. On each side of the 24 cu, we have two 40 cu (one 40 cu is 4 cu plus 16 cu plus 20 cu), and finally we have a single 32 cu. A good one.