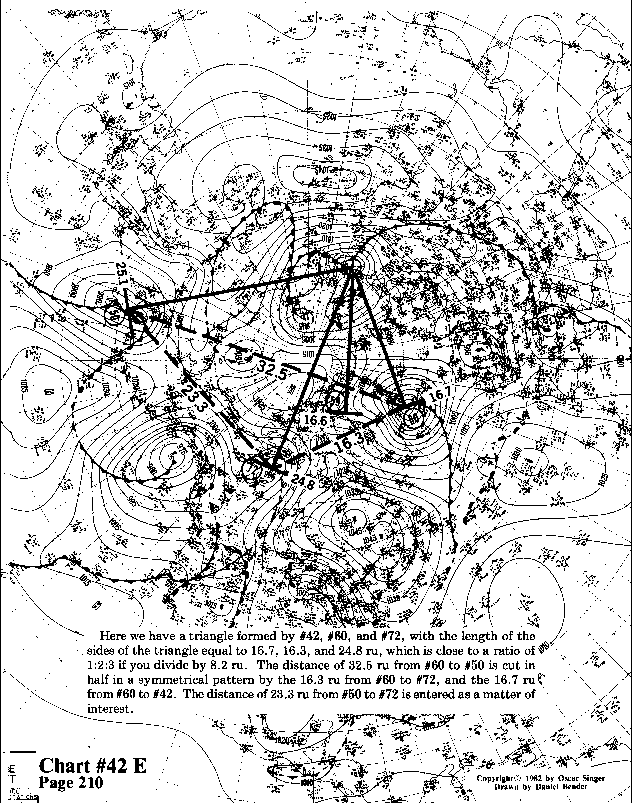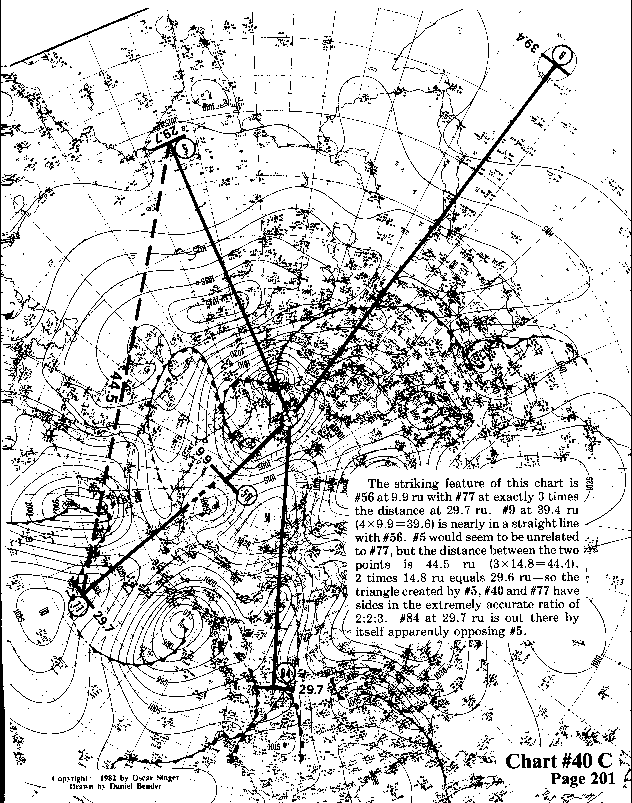
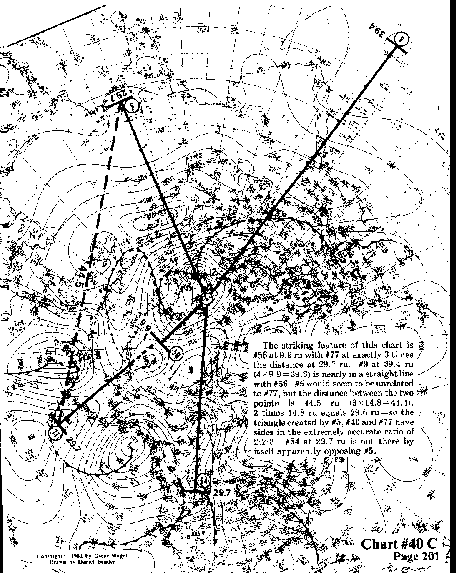
The striking feature of this chart is #56 at 9.9 ru with #77 at
exactly 3 times the distance at 29.7 ru. #9 at 39.4 ru (4 x 9.9 = 39.6) is nearly in a straight
line with #56. #5 would seem to be unrelated to #77, but the distance
between the two points is 44.5 ru (3 X 14.8 = 44.4).
2 times 14.8 ru equals 29.6 ru--so the triangle created by #5, #40 and #77 have sides
in the extremely accurate ratio of 2:2:3. #84 at 29.7 ru is out there by itself apparently opposing #5.
#84, #77, and #5 are part of a vortex wavefront at a distance of 29.7 ru.

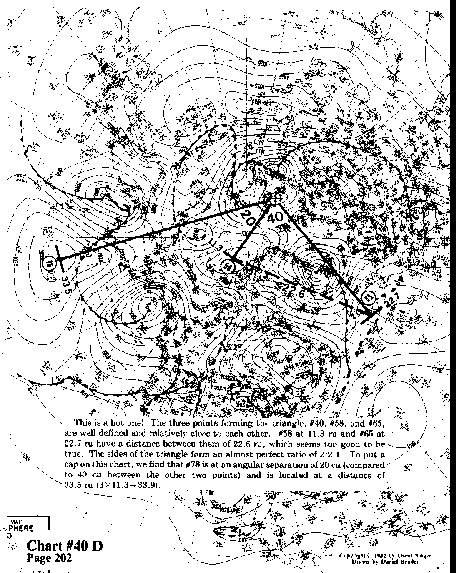
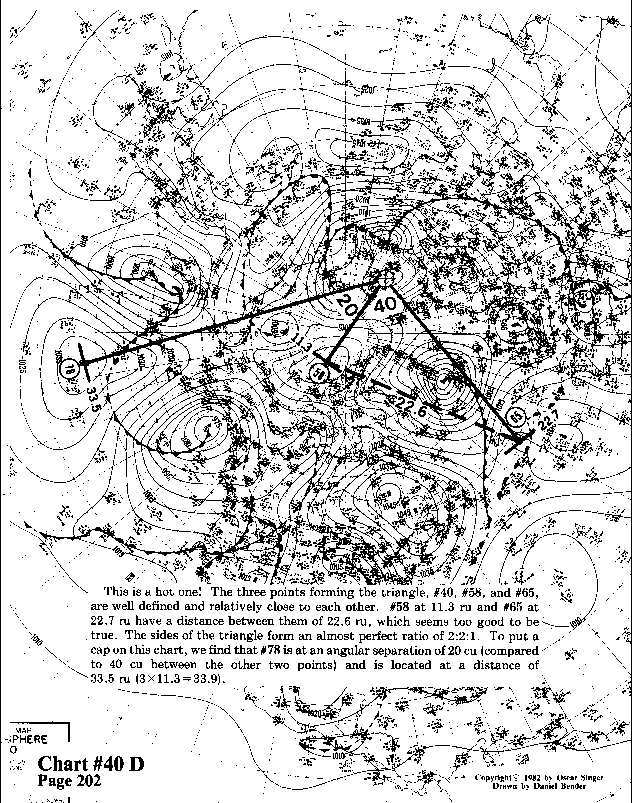
This is a hot one! The three points forming the triangle, #40,
#58, and #65, are well defined and relatively close to each other.
#58 at 11.3 ru and #65 at 22.7 ru have a distance between them
of 22.6 ru, which seems too good to be; true. The sides of the
triangle form an almost perfect ratio of 2:2:1. To put a cap on
this chart, we find that #78 is at an angular separation of 20
cu (compared to 40 cu between the other two points) and is located
at a distance of 33.5 ru (3 x 11.3 = 33.9).
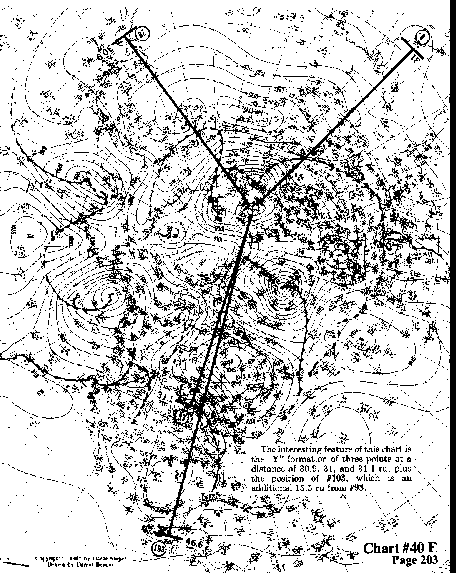
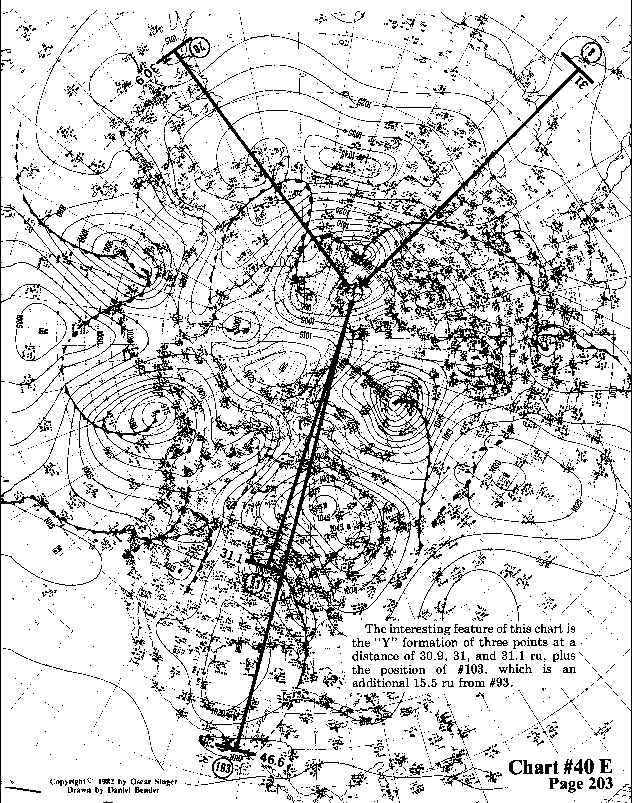
The interesting feature of this chart is the"Y" formation
of three points at a distance of 30.9, 31, and 31.1 ru, plus .
the position of #103, which is an additional 15.5 ru from #93.
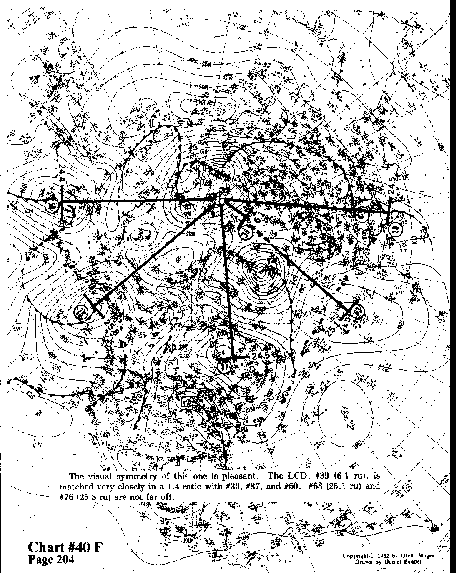
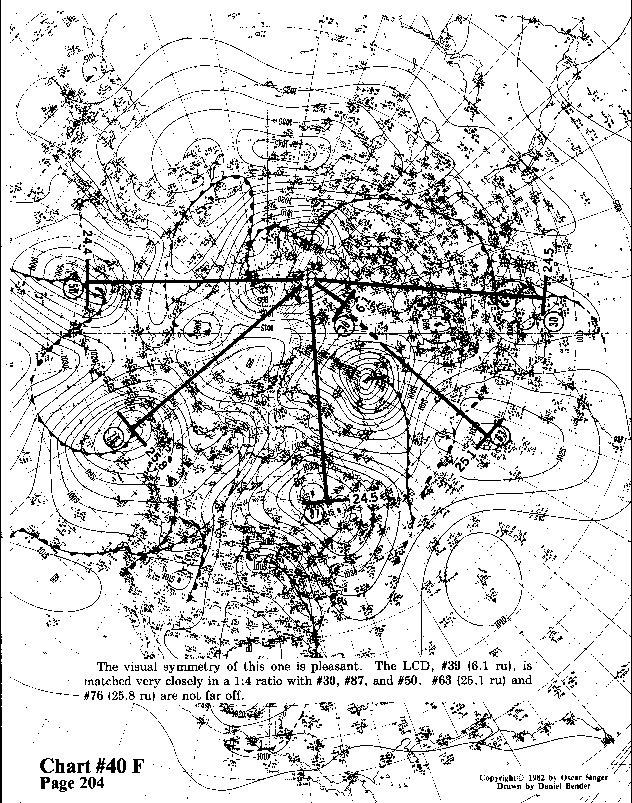
The visual symmetry of this one is pleasant. The LCD, #39 (6.1ru),
is matched very closely in a 1:4 ratio with #30, #87, and
#50. #63 (25.1 ru) and #76 (25.8 ru) are not far off.
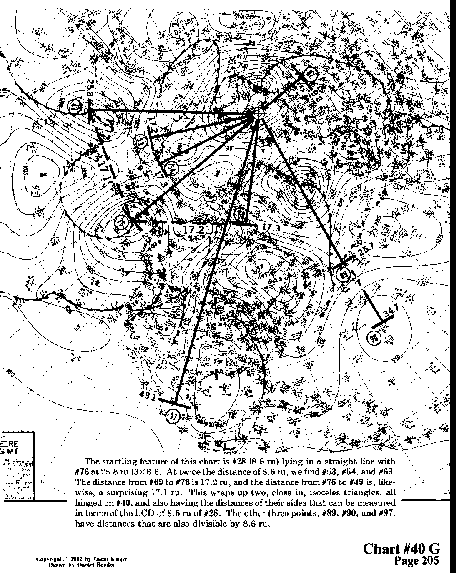
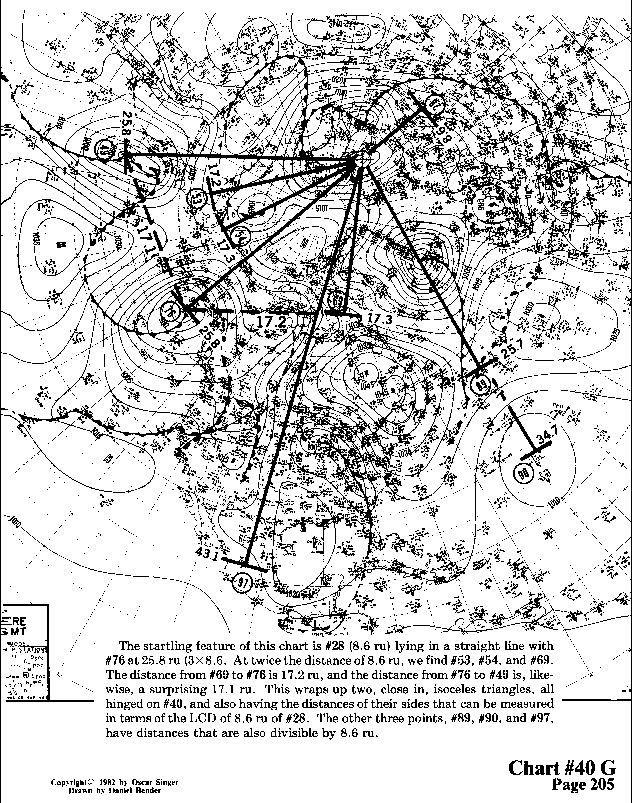
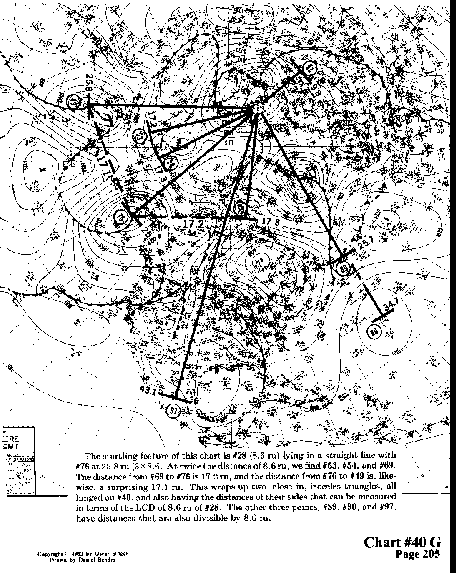
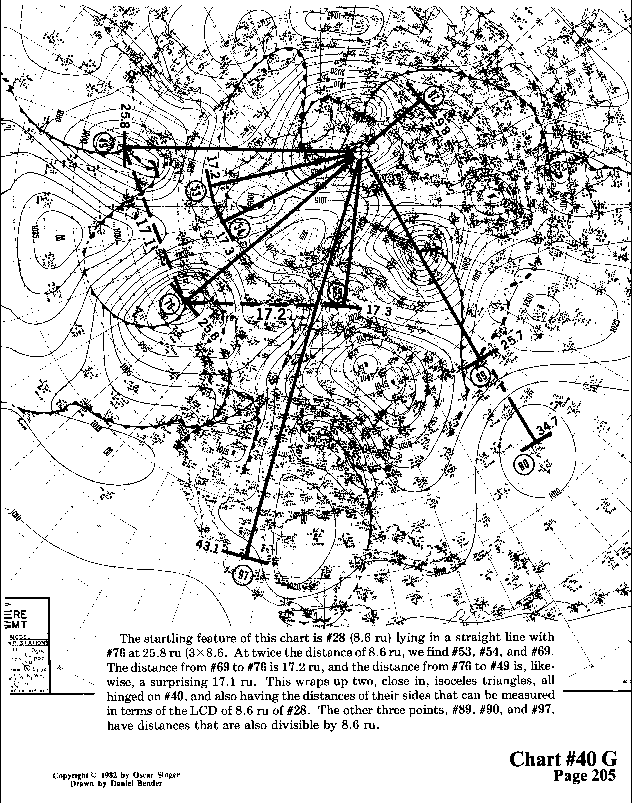
The startling feature of this chart is #28 (8.6 ru) lying in a
straight line with #76 at 25.8 ru (3 x 8.6). At twice the distance
of 8.6 ru, we find #53, #54, and #69. The distance from #69 to
#76 is 17.2 ru, and the distance from #76 to #49 is, likewise,
a surprising 17.1 ru. This wraps up two, close in, isoceles triangles,
all hinged on #40, and also having the distances of their sides
that can be measured in terms of the LCD of 8.6 ru of #28. The
other three points, #89, #90, and #97, have distances that are
also divisible by 8.6 ru.
One unusual feature of this chart is #45 (8 ru), #55 (16 ru, and #52 (23.9 ru).
These distances are in a spacing of 1:2:3 radiating outwards in the same general direction from
#42. Another unusual feature is #29 at 12.1 ru doubling to 24.2 ru exactly for #51 on the other
side of #42. All the remaining points have the distances divisible
by an LCD of 4 or 8 ru as the individual case may warrant.
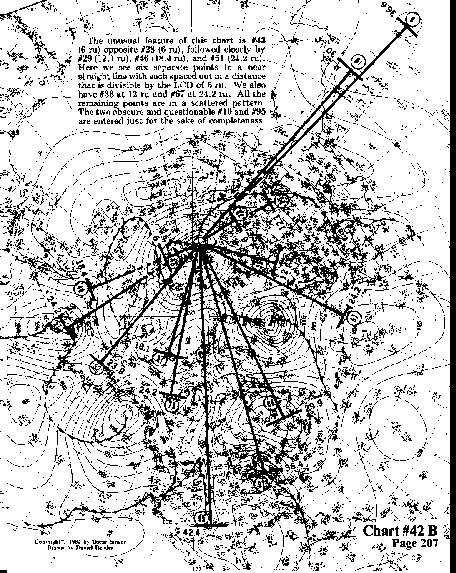
The unusual feature of this chart is #43 (6 ru) opposite #28 (6 ru),
followed closely by #29 (12.1 ru), #46 (18.4 ru), and #51 (24.2 ru).
Here we see six separate points in a near straight
line with each spaced out in a distance that is divisible by the
LCD of 6 ru. We also have #36 at 12 ru and #67 at 24.2 ru.
All the remaining points are in a scattered pattern. The two obscure
and questionable #10 and #95 are entered just for the sake of completeness.

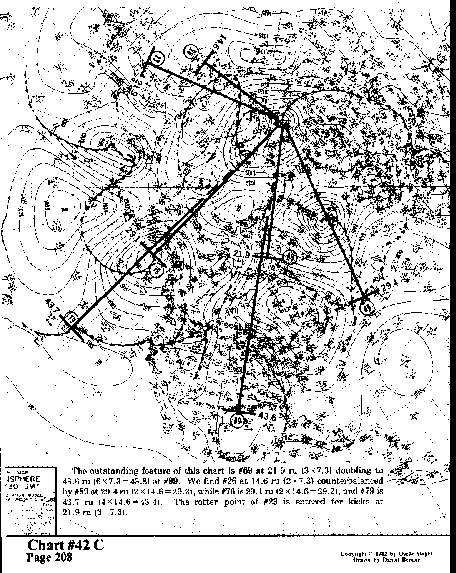
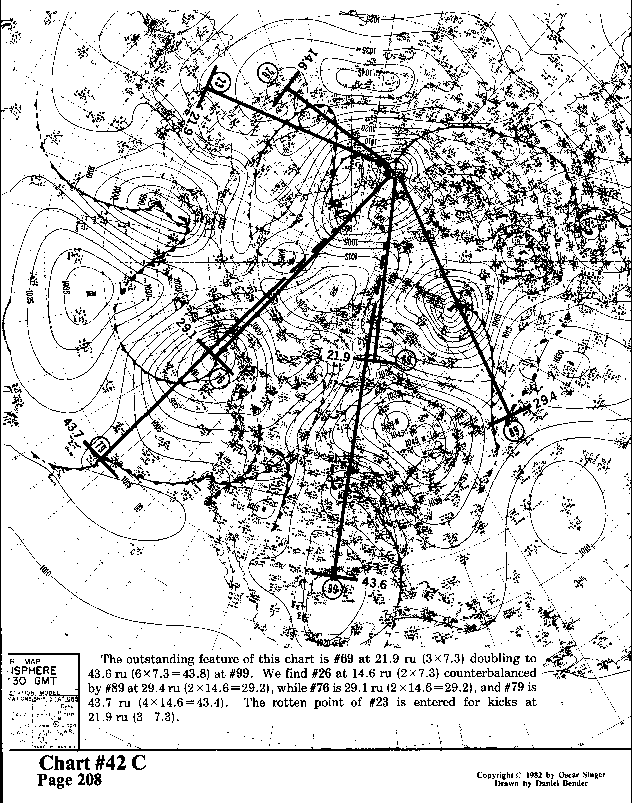
The outstanding feature of this chart is #69 at 21.9 ru (3x7.3)
doubling to 43.6 ru (6 x 7.3 = 43.8) at #99. We find #26 at
14.6 ru (2 x 7.3) counterbalanced by #89 at 29.4ru (2x14.6=29.2),
while#76 is 29.1 ru (2x14.6=29.2), and #79 is 43.7 ru (4x14.6=43.4).
The rotten point of #23 is entered for kicks at
21.9 ru (3x7.3).
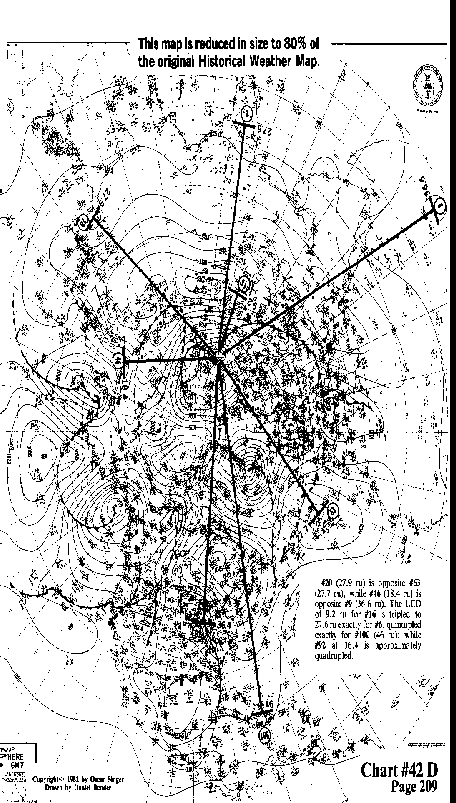
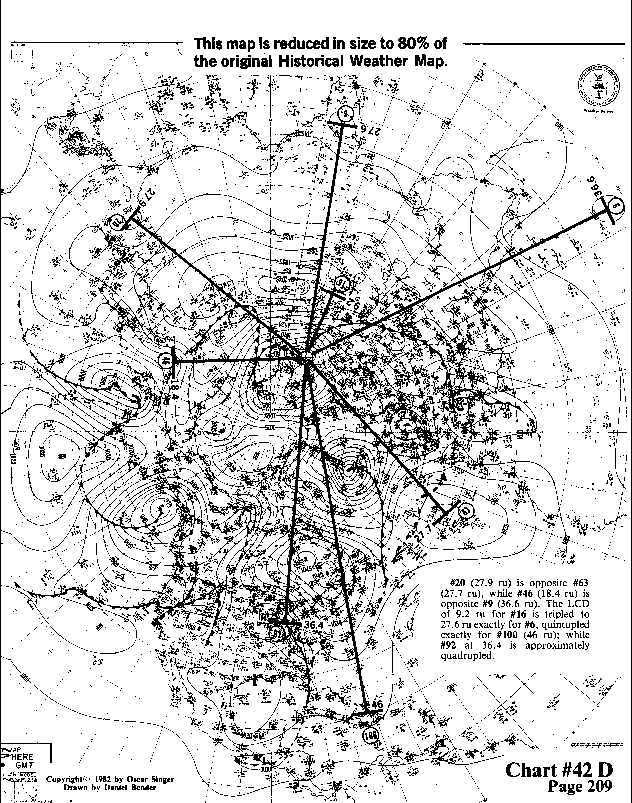
#20 (27.9 ru) is opposite #63 (27.7 ru), while #46 (18.4 ru) is
opposite #9 (36.6 ru). The LCD of 9.2 ru for #16 is tripled to
27.6 ru exactly for #6, quintupled exactly for #100 (46 ru) while
#92 at 36.4 is approximately quadrupled.
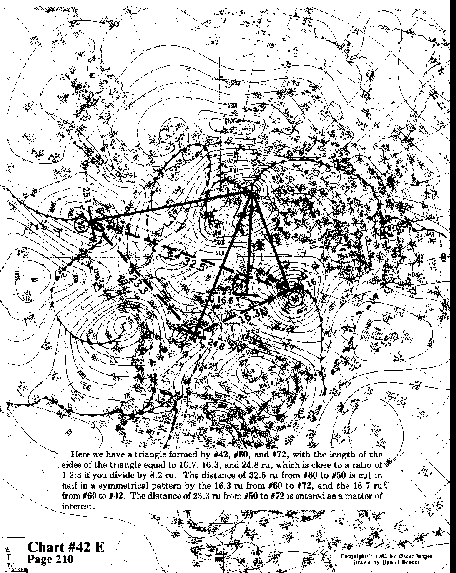
Here we have a triangle formed by #42, #60, and #72, with the
length of the sides of the triangle equal to 16.7, 16.3, and 24.8
ru, which is close to a ratio of 1:2:3 if you divide by 8.2
ru. The distance of 32.5 ru from #60 to #50 is cut in half in
a symmetrical pattern by the 16.3 ru from #60 to #72, and the
16.7 ru from #60 to #42. The distance of 23.3 ru from #50 to #72
is entered as a matter of interest.