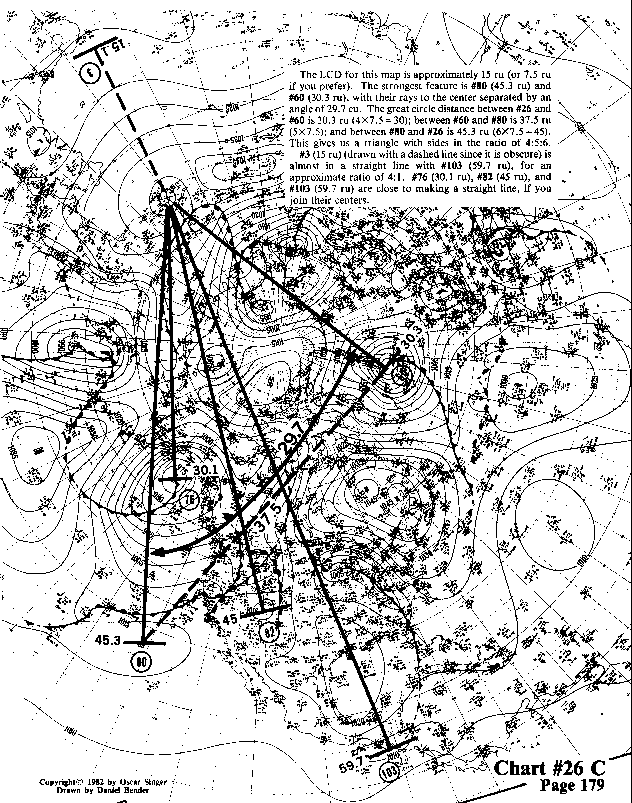
The LCD for this map is approximately 15 ru (or 7.5 ru if you prefer). The strongest feature is #80 (45.3 ru) and #60 (30.3 ru), with their rays to the center separated by an angle of 29.7 cu. The great circle distance between #26 and #60 is 30.3 ru (4x7.5 = 30); between #60 and #80 is 37.5 ru (5x7.5); and between #80 and #26 is 45.3 ru (6x7.5=45). This gives us a triangle with sides in the ratio of 4:5:6. #3 (15 ru) (drawn with a dashed line since it is obscure) is almost in a straight line with #103 (59.7 ru), for an approximate ratio of 4:1. #76 (30.1 ru), #82 (45 ru), and #103 (59.7 ru) are close to making a straight line, if you join their centers.

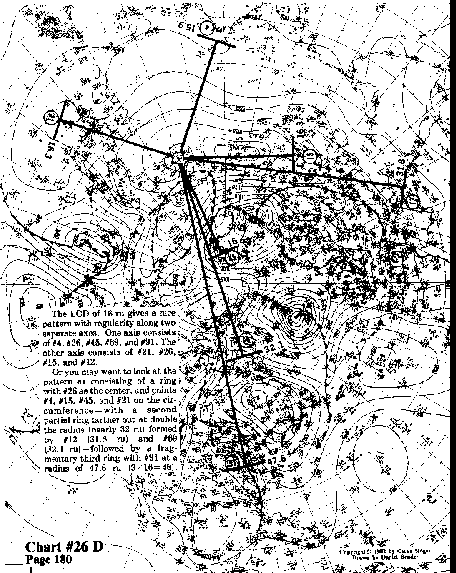
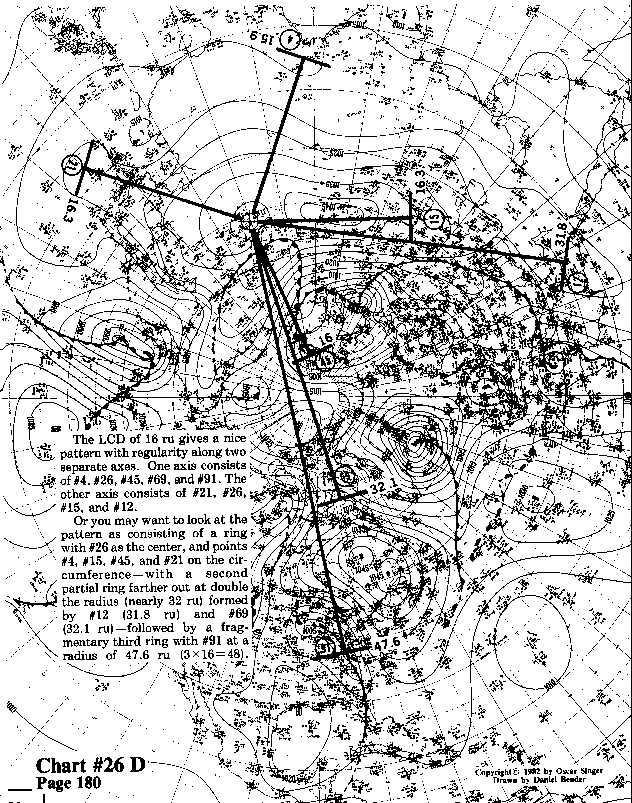
The LCD of 16 ru gives a nice pattern with regularity along two separate axes. One axis consists of #4, #26, #45, #69, and #91. The other axis consists of #21, #26, #15, and#l2.

Or you may want to look at the pattern as consisting of a ring with #26 as the center, and points #4, #15, #45, and #21 on the circumference--with a second partial ring farther out at double the radius (nearly 32 ru) formed by #12 (31.8 ru) and #69 (32.1 ru)--followed by a fragmentary third ring with #91 at a radius of 47.6 ru (3x16=48).

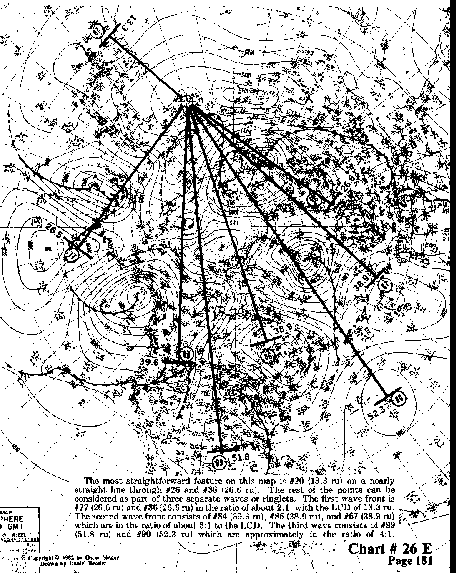
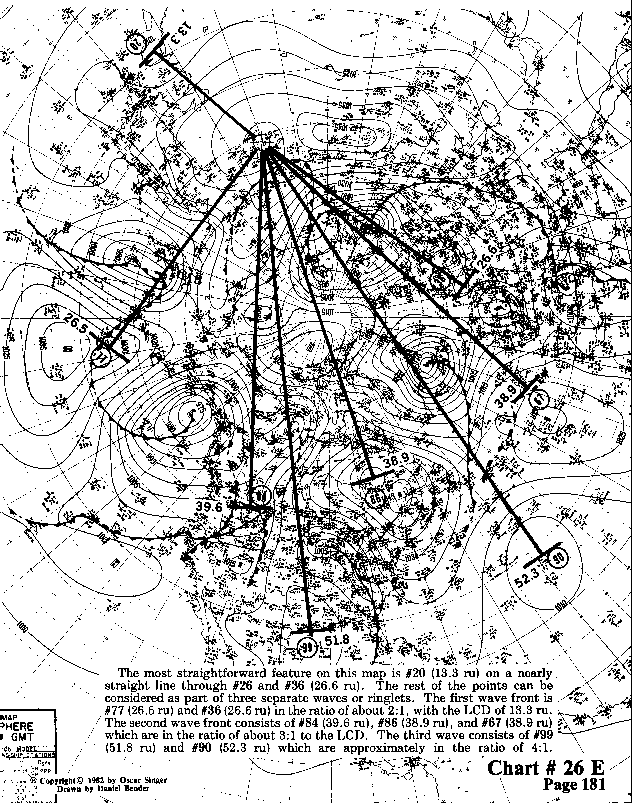
The most straightforward feature on this map is #20 (13.3 ru) on a nearly straight line through #26 and #36 (26.6 ru). The rest of the points can be considered as part of three separate waves or ringlets. The first wave front is, #77 (26.5 ru) and #36 (26.6 >ru) in the ratio of about 2:1, with the LCD of 13.3 ru. The second wave front consists of #84 (39.6 ru), #86 (38.9 ru), and #67 (38.9 ru) which are in the ratio of about 3:1 to the LCD. The third wave consists of #99 (51.8 ru) and #90 (52.3 ru) which are approximately in the ratio of 4:1.

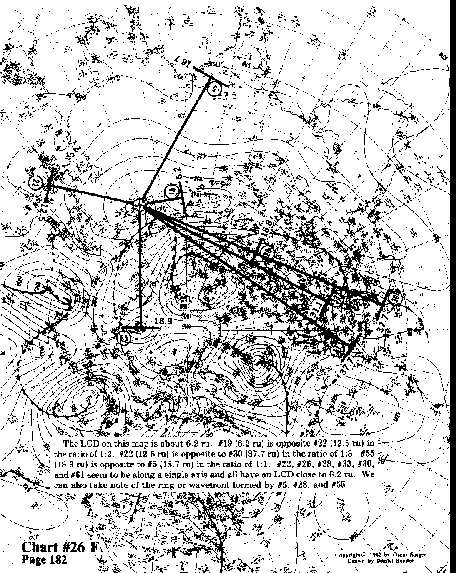
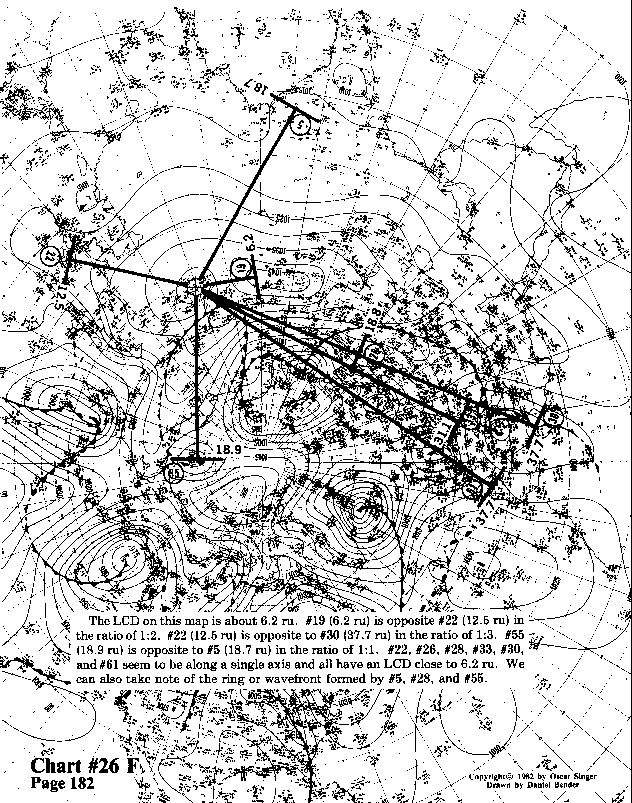
The LCD on this map is about 6.2 ru. #19 (6.2 ru) is opposite #22 (12.5 ru) in the ratio of 1:2. #22 (12.5 ru) is opposite to #30 (37.7 ru) in the ratio of 1:3. #55 (18.9 ru) is opposite to #5 (18.7 ru) in the ratio of 1:1. #22, #26, #28, #33, #30, and #61 seem to be along a single axis and all have an LCD close to 6.2 ru. We can also take note of the ring or wavefront formed by #5, #28, and #55.

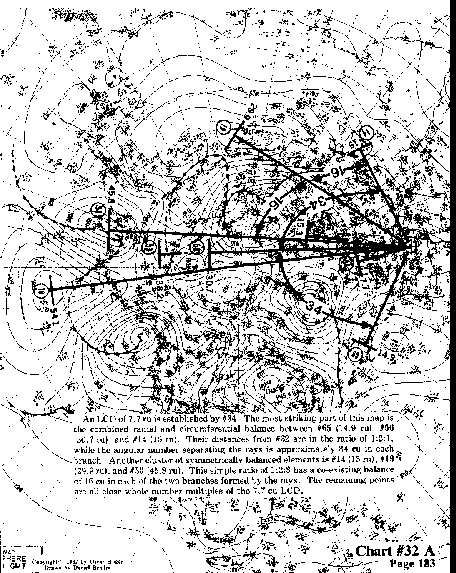
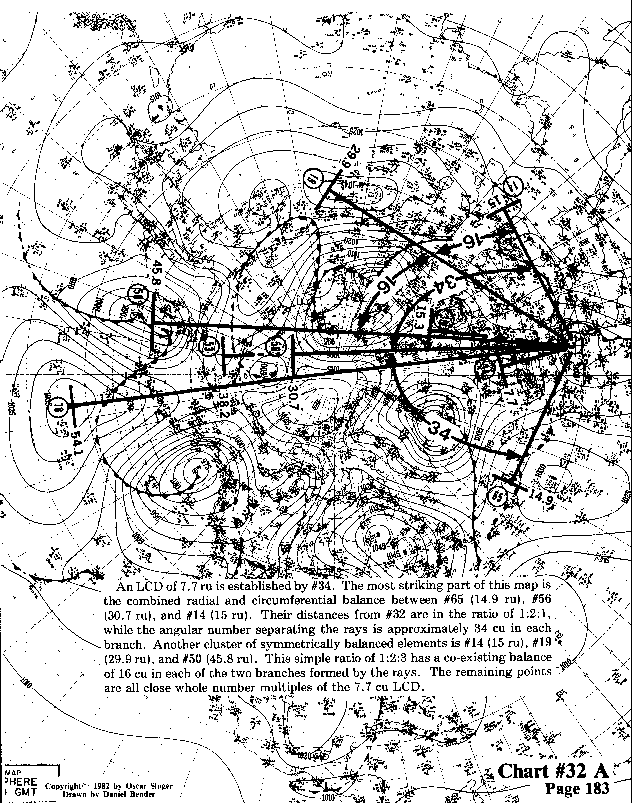
An LCD of 7.7 ru is established by #34. The most striking part of this map is the combined radial and circumferential balance between #65 (14.9 ru), #56 (30.7 ru), and #14 (15 ru). Their distances from #32 are in the ratio of 1:2:1, while the angular number separating the rays is approximately 34 cu in each branch. Another cluster of symmetrically balanced elements is #14 (15 ru), #19 (29.9 ru), and #50 (45.8 ru). This simple ratio of 1:2:3 has a coexisting balance of 16 cu in each of the two branches formed by the rays. The remaining points are all close whole number multiples of the 7.7 cu LCD.

We are not through with this beauty--the distance between #20 and #9 (also with a well-defined location for the center) is 47.1 ru. Since #9 is 24 ru from #32, we have an isoceles triangle with the sides in the approximate ratio of 2:2:1 as a very neat companion to the first triangle.

We can't quit now, since #9 (24 ru) is counterbalanced in an almost straight line by #97 (47.8 ru) in a nearly perfect 1:2 ratio.

What have we here! Another equilateral triangle? This time, #97,#47 and #32 are locked in close balance, since the dashed line between #97 and #47 indicates a distance of 49.1 ru-not as perfect as the first triangle, but good.

We still can't let go of #97. The distance between #97 and #63 is 35.8 ru; between #97 and #20 is 60.1 ru; and between #97 and #8 is 71.6 ru. All these distances are multiples of the LCD, 12 ru. There are five different distances radiating out from #97 to different members of this cluster of points that have a common LCD of 12 ru--not bad for a point like #97, that most meteorologists might have thought to be of no significance and without merit.

To wrap up this dazzler, we see that #90 at 24.6 ru is almost perfectly counterbalanced in a nearly straight line with #8 at 24.7 ru (with #63 at 12.7 ru acting as an interloper). We see that there is a ring or wavefront involving #90 (24.6 ru), #44 (24.6 ru), #7 (24.6 ru), #8 (24.7 ru), and #9 (24 ru). Lastly, #93 at 36.2 ru and #100 at 36.4 ru form another ringlet. We can't tarry much longer with this chart, since there are other areas of the map to investigate.

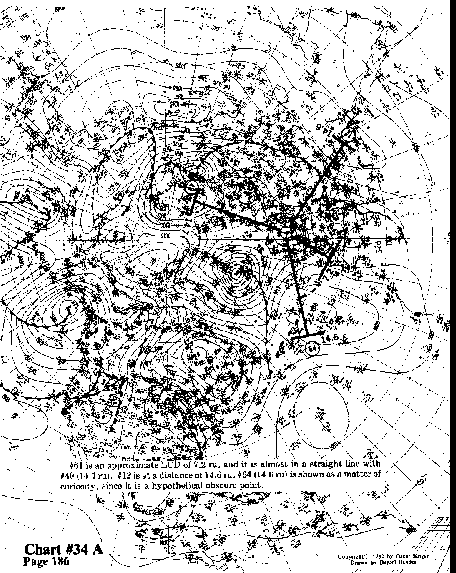
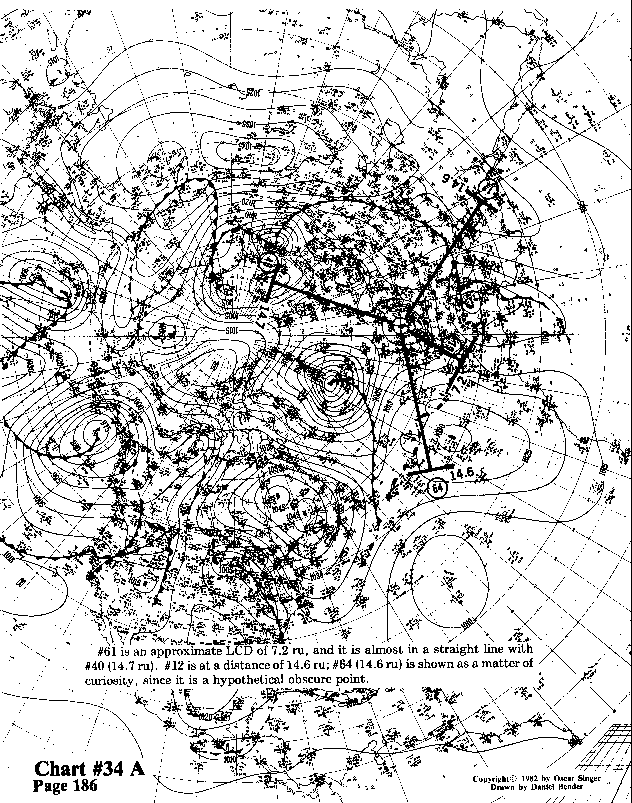
#61 is an approximate LCD of 7.2 ru, and it is almost in a straight line with #40 (14.7 ru). #12 is at a distance of 14.6 ru; #64 (14.6 ru) is shown as a matter of curiosity, since it is a hypothetical obscure point.

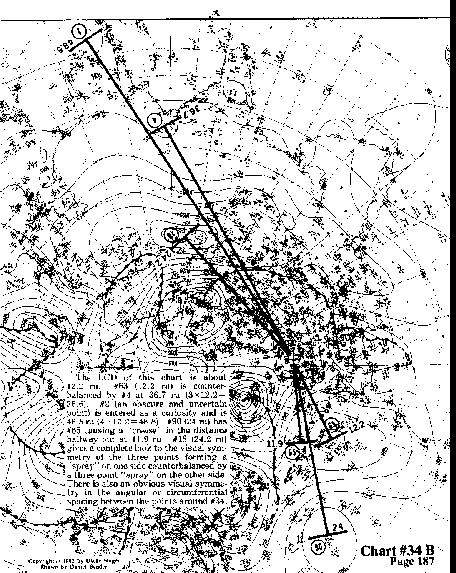
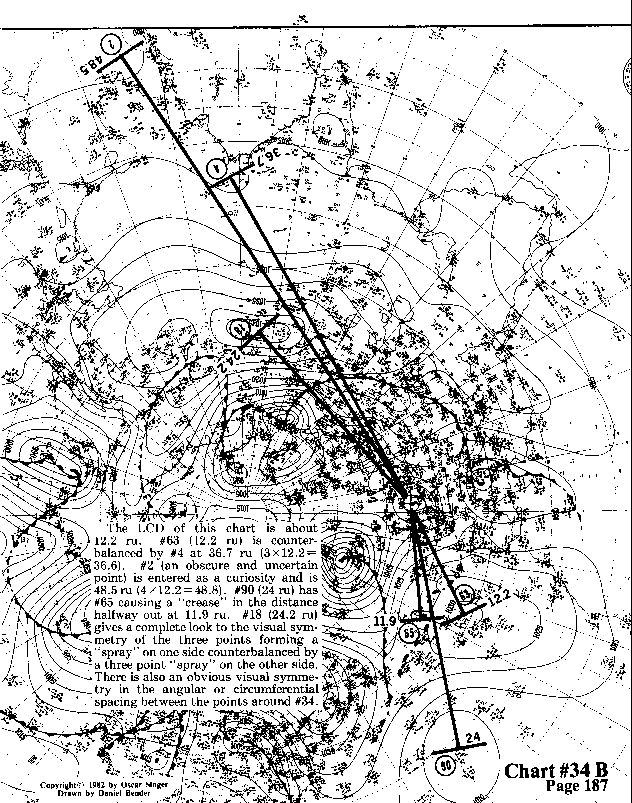
The LCD of this chart is about 12.2 ru. #63 (12.2 ru) is counterbalanced by #4 at 36.7 ru (3x12.2=36.6). #2 (an obscure and uncertain point) is entered as a curiosity and is 48.5 ru (4 x12.2 =48.8). #90 (24 ru) has #65 causing a "crease" in the distance halfway out at 11.9 ru. #18 (24.2 ru) gives a complete look to the visual symmetry of the three points forming a "spray" on one side counterbalanced by a three point "spray" on the other side. There is also an obvious visual symmetry in the angular or circumferential spacing between the points around #34.

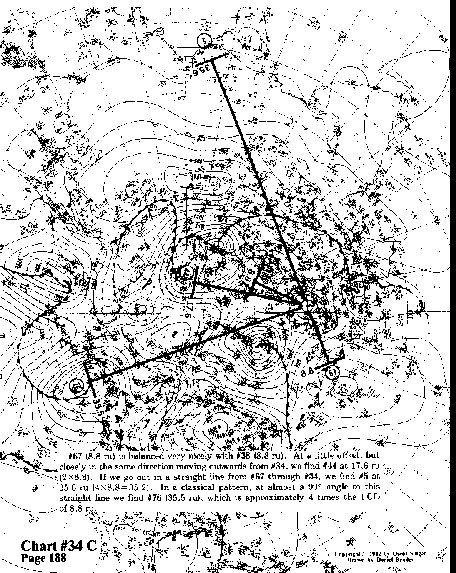
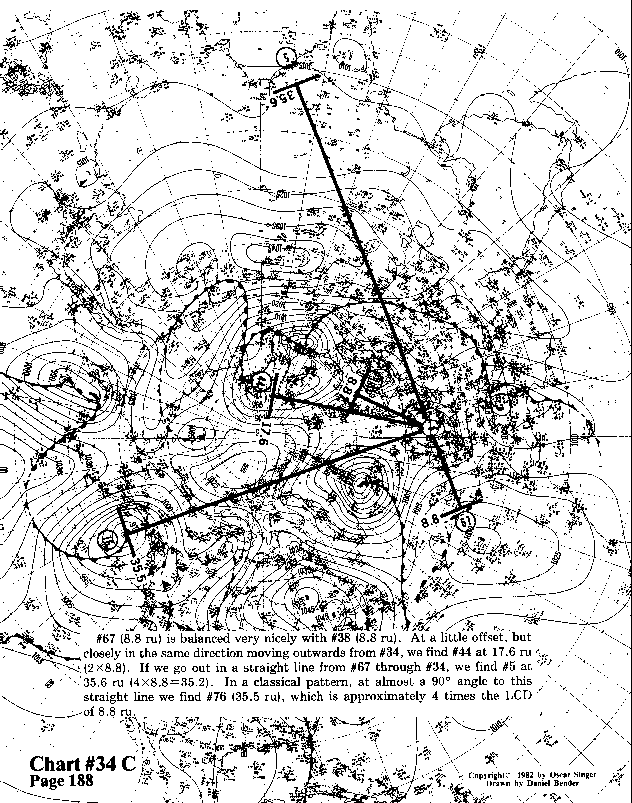
#67 (8.8 ru) is balanced very nicely with #38 (8.8 ru). At a little offset, but closely in the same direction moving outwards from #34, we find #44 at 17.6 ru (2x8.8). If we go out in a straight line from #67 through #34, we find #5 at 35.6 ru (4x8.8=35.2). In a classical pattern, at almost a 90° angle to this straight line we find #76 (35.5 ru), which is approximately 4 times the LCD of 8.8 ru.

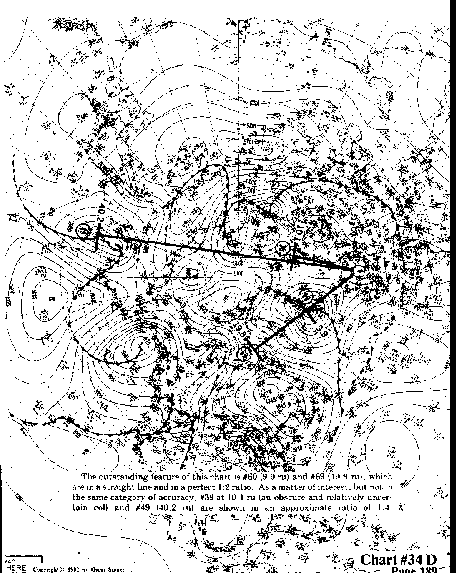
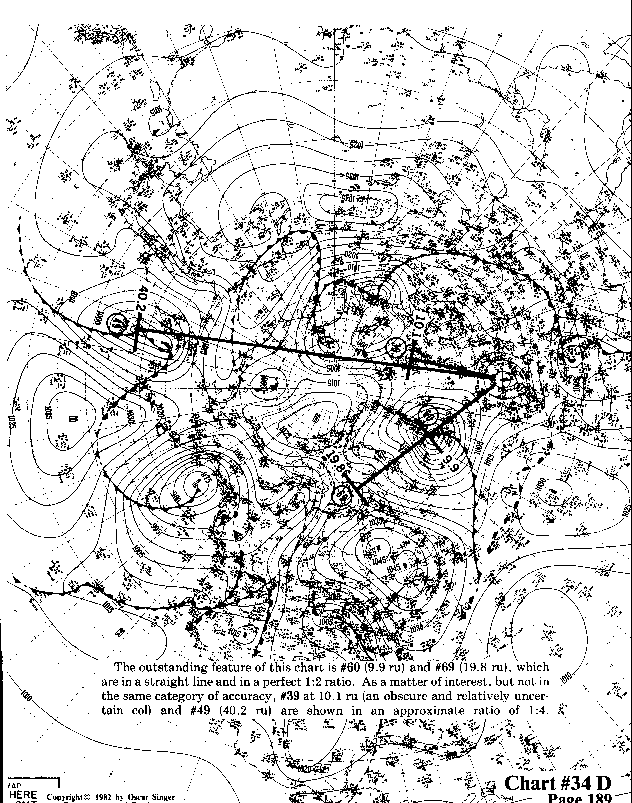
The outstanding feature of this chart is #60 (9.9 ru) and #69 (19.8 ru), which are in a straight line and in a perfect 1:2 ratio. As a matter of interest, but not in the same category of accuracy, #39 at 10.1 ru (an obscure and relatively uncertain col) and #49 (40.2ru) are shown in an approximate ratio of 1:4.

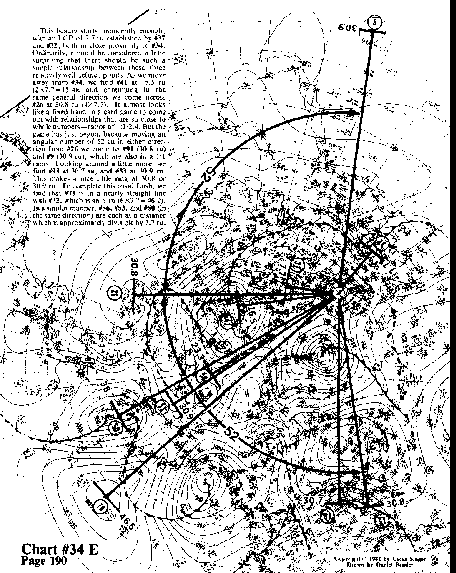
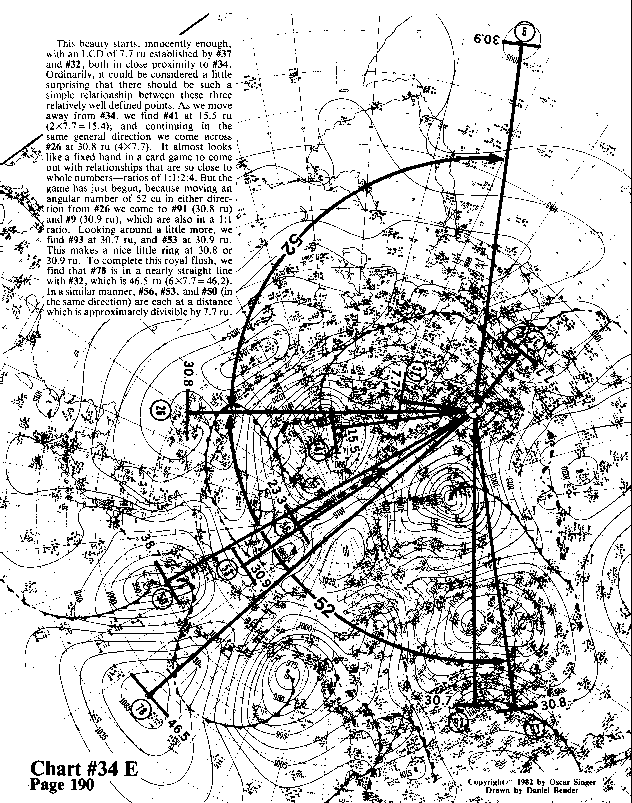
This beauty starts, innocently enough, with an LCD of 7.7 ru established by #37 and #32 both in close proximity to #34. Ordinarily, it could be considered a little surprising that there should be such a simple relationship between these three relatively well defined points. As we move away from #34, we find #41 at 15.5 ru (2X7.7= 15.4); and continuing in the same general direction we come across #26 at 30.8 ru (4X7.7)--a distance of 3465 nautical miles. It almost looks like a fixed hand in a card game to come out with relationships that are so close to whole numbers--ratios of 1:1:2:4. But the . game has just begun, because moving an angular number of 52 cu in either direction from #26 we come to #91 (30.8 ru) and #9 (30.9 ru), which are also in a 1:1 ratio. Looking around a little more, we find #93 at 30.7 ru, and #53 at 30.9 ru. This makes a nice little ring or wave front of vortexes at 30.8 or 30.9 ru. To complete this royal flush, we find that #78 is in a nearly straight line with #32, which is 46.5 ru (6X7.7 = 46.2). In a similar manner, #56, #53, and #50 (in the same direction) are each at a distance which is approximately divisible by 7.7 ru.

This one is a masterpiece of hemispheric precision.