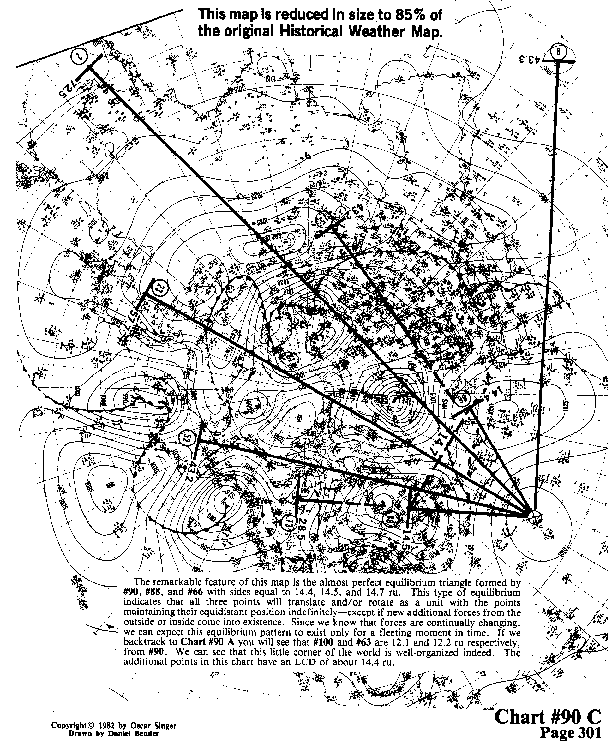
The remarkable feature of this map is the almost perfect equilibrium triangle formed by #90, #88, and #66 with sides equal to 14.4, 14.5, and 14.7 ru. This type of equilibrium indicates that all three points will translate and/or rotate as a unit with the points maintaining their equidistant position indefinitely-except if new additional forces from the outside or inside come into existence. Since we know that forces are continually changing, we can expect this equilibrium pattern to exist only for a fleeting moment in time. If we backtrack to #90 A you will see that #100 and #63 are 12.1 and 12.2 ru respectively, from #90. We can see that this little corner of the world is well-organized indeed. The additional points in this chart have an LCD of about 14.4 ru.
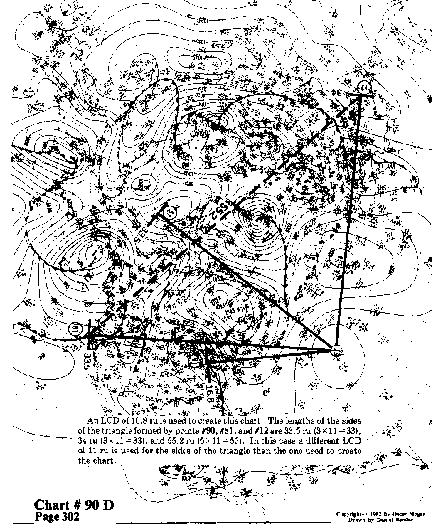
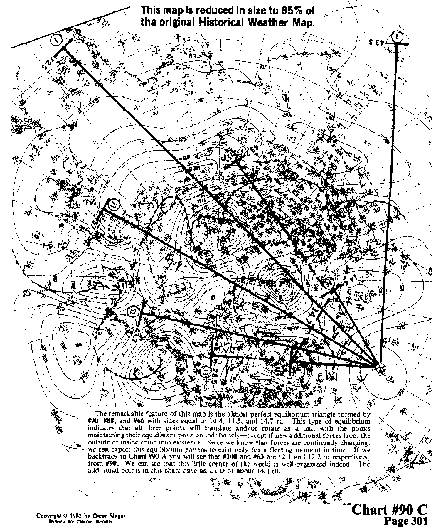
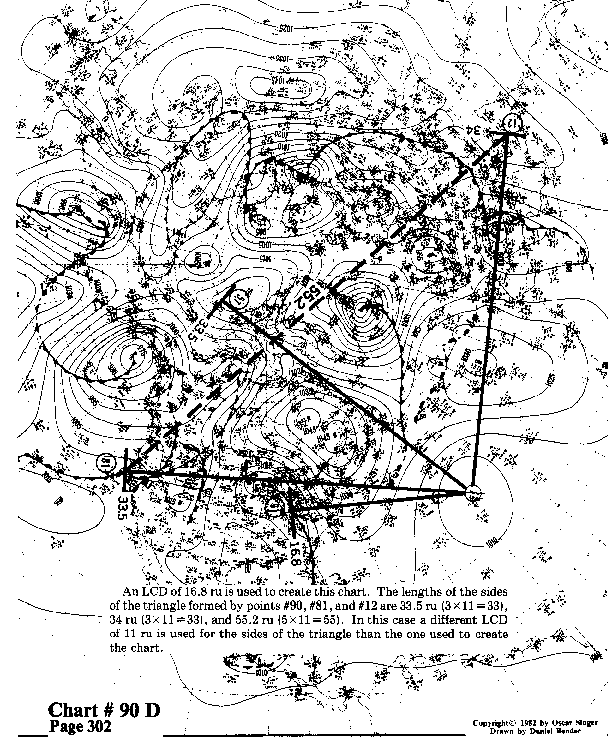
An LCD of 16.8 ru is used to create this chart. The lengths of the sides of the triangle formed by points #90, #81, and #12 are 33.5 ru (3 x 11=33), 34 ru (3x 11=33), and 55.2 ru (5 x 11=55). In this case a different LCD of 11 ru is used for the sides of the triangle than the one used to create the chart.
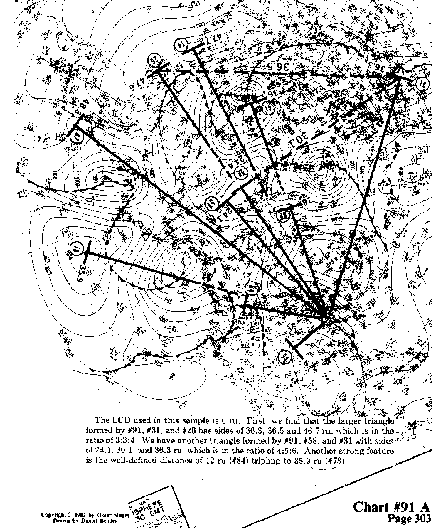
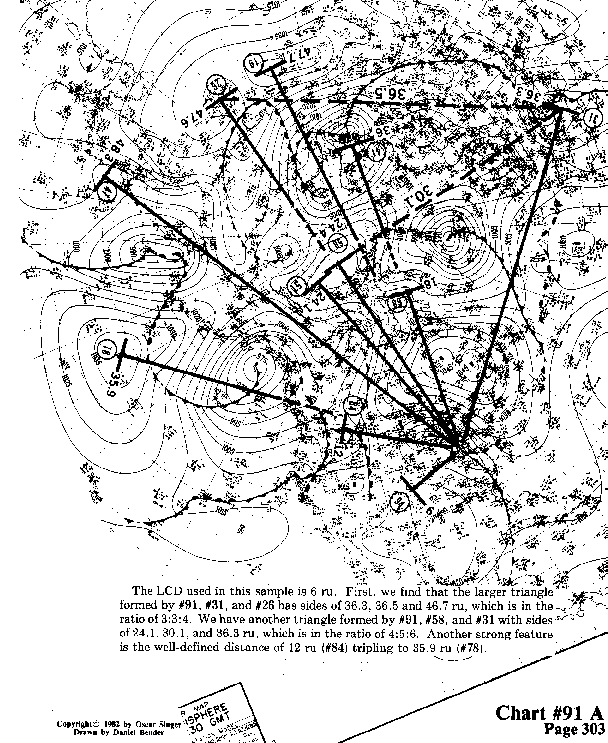
The LCD used in this sample is 6 ru. First, we find that the larger
triangle formed by #91, #31, and #26 has sides of 36.3, 36.5
and 46.7 ru, which is in the ratio of 3:3:4. We have another
triangle formed by #91, #58, and #31 with sides s of 24.1, 30.1,
and 36.3 ru, which is in the ratio of 4:5:6. Another strong feature
is the well-defined distance of 12 ru (#84) tripling to 35.9 ru (#78).

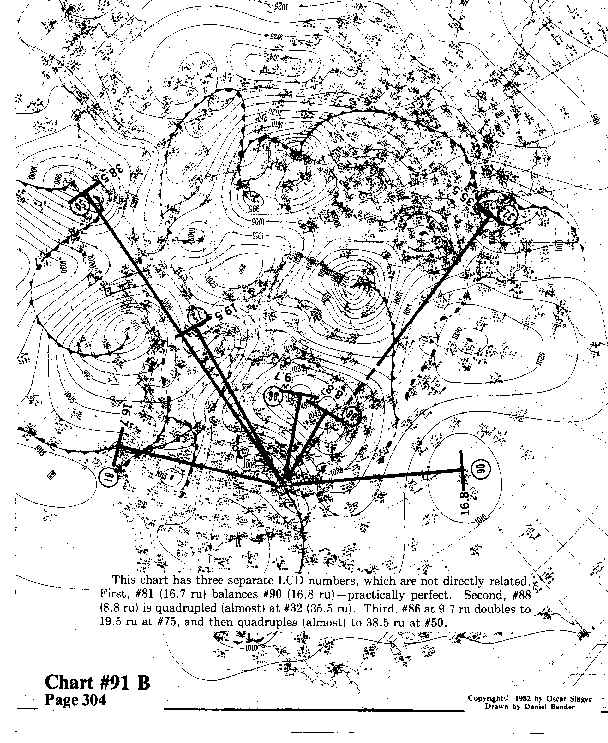
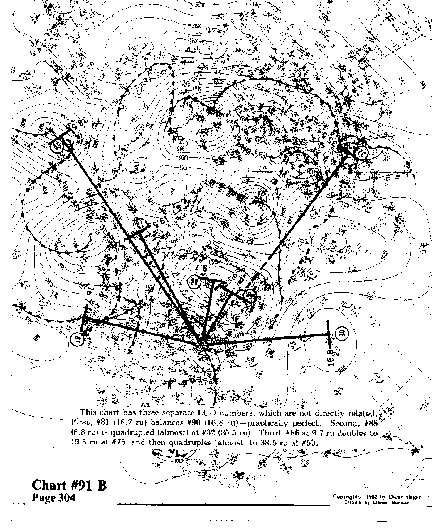 This chart has three separate LCD numbers, which are not directly
related. First, #81 (16.7 ru) balances #90 (16.8 ru)-practically
perfect. Second, #88 (8.8 ru) is quadrupled (almost) at #32 (35.5
ru). Third, #86 at 9.7 ru doubles to 19.5 ru at #75, and then
quadruples (almost) to 38.5 ru at #50.
This chart has three separate LCD numbers, which are not directly
related. First, #81 (16.7 ru) balances #90 (16.8 ru)-practically
perfect. Second, #88 (8.8 ru) is quadrupled (almost) at #32 (35.5
ru). Third, #86 at 9.7 ru doubles to 19.5 ru at #75, and then
quadruples (almost) to 38.5 ru at #50.
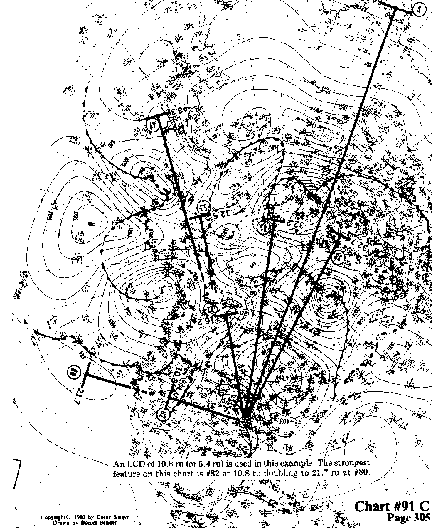
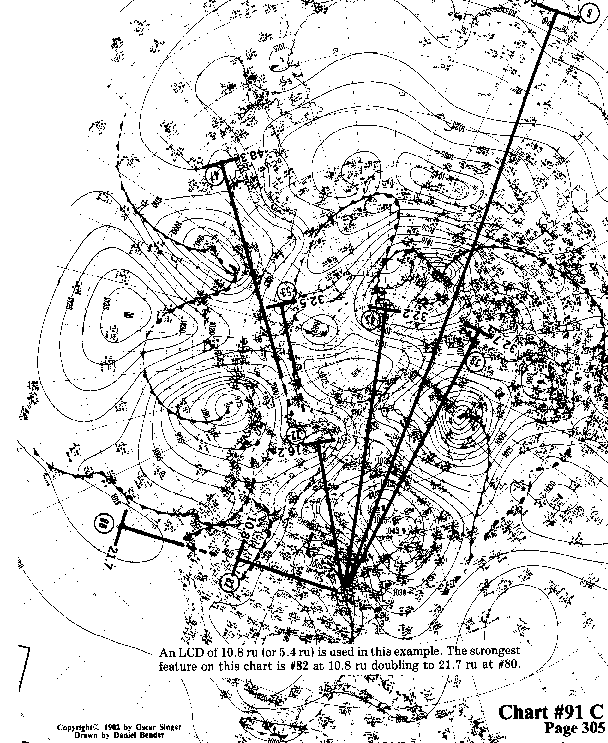
An LCD of 10.8 ru (or 5.4 ru) is used in this example. The strongest
feature on this chart is #82 at 10.8 ru doubling to 21.7 ru at #80.
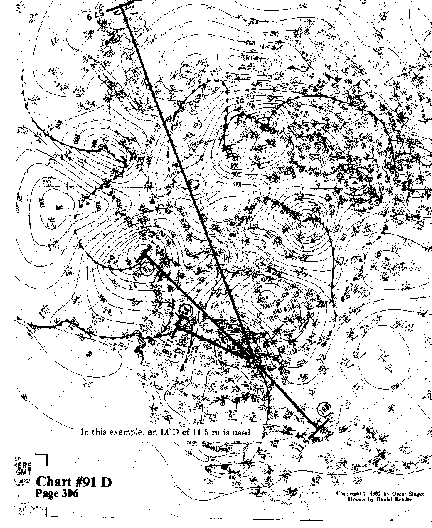
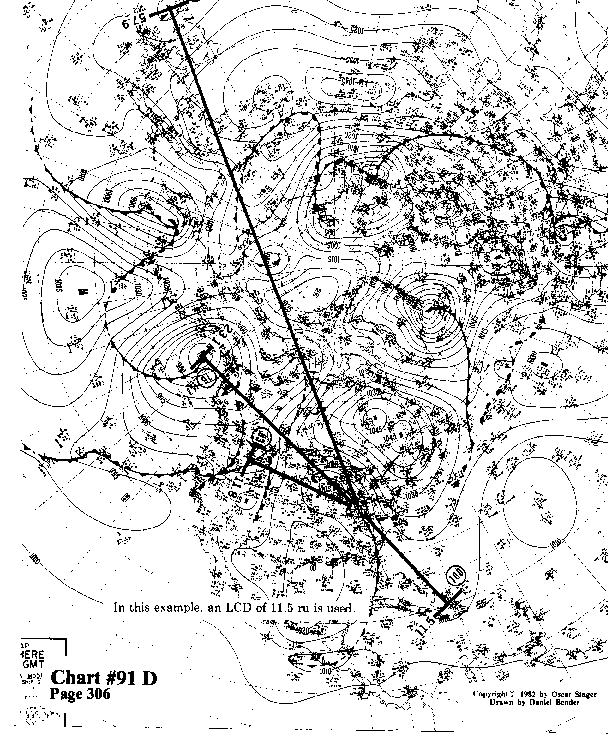
In this example, an LCD of 11.5 ru is used.
 This example
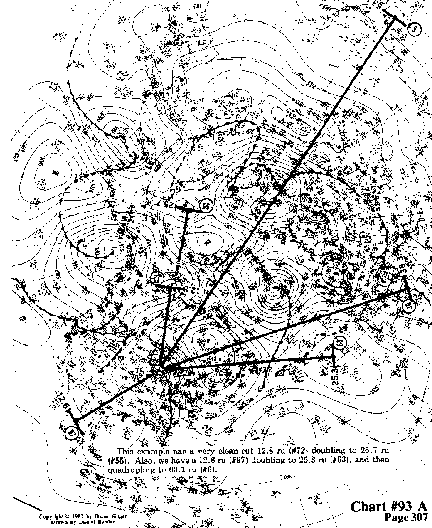
has a very cleancut 12.8 ru (#72) doubling to 25.7 ru (#55).
Also, we have a 12.6 ru (#97) doubling to 25.3 ru (#63), and then
quadrupling to 63.1 ru (#6).
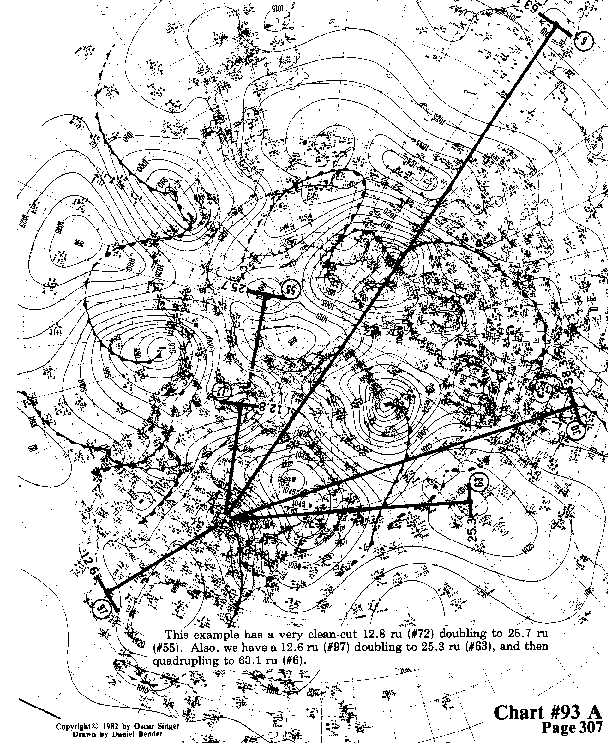
This example
has a very cleancut 12.8 ru (#72) doubling to 25.7 ru (#55).
Also, we have a 12.6 ru (#97) doubling to 25.3 ru (#63), and then
quadrupling to 63.1 ru (#6).
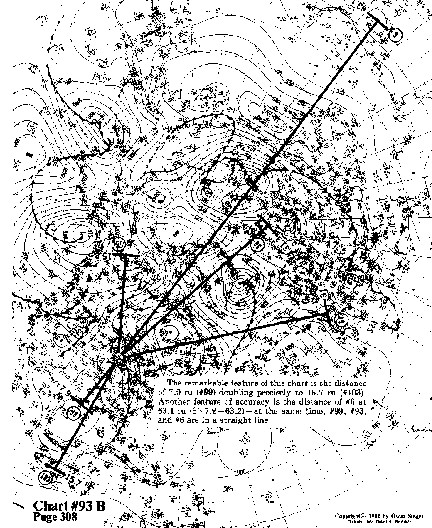
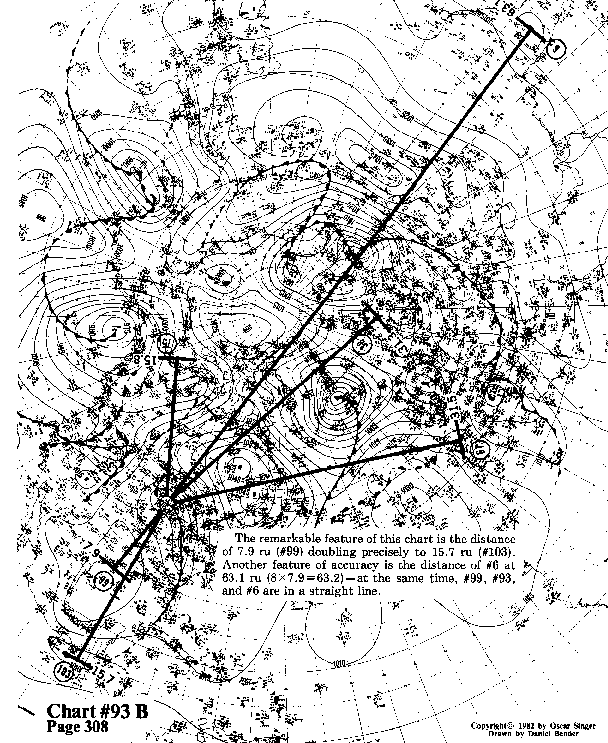
The remarkable feature of this chart is the distance of 7.9 ru
(#99) doubling precisely to 15.7 ru (#103). Another feature of
accuracy is the distance of #6 at 63.1 ru (8x7.9=63.2)-at the
same time, #99, #93, and #6 are in a straight line.
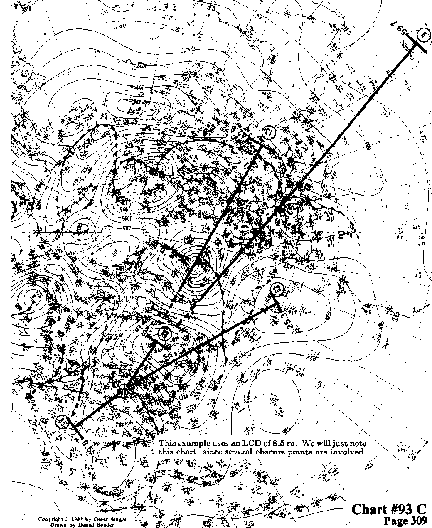
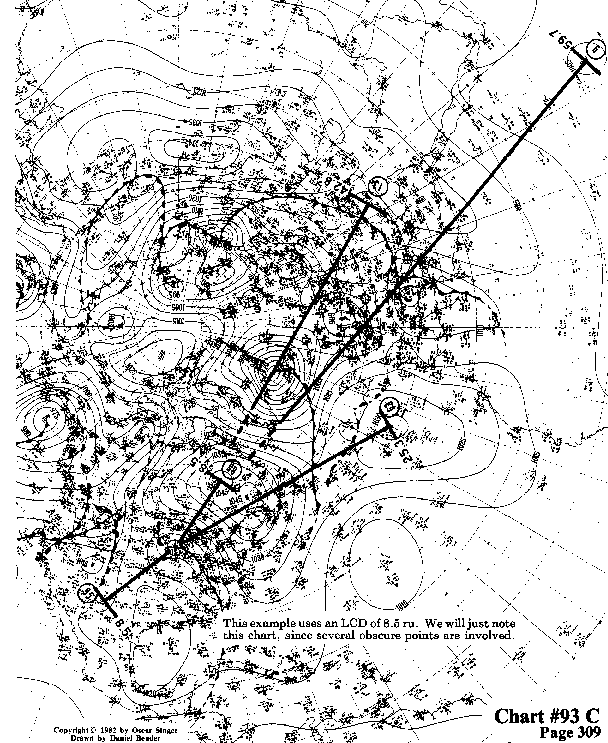
This example uses an LCD of 8.5 ru We will just note this chart,
since several obscure points are involved.
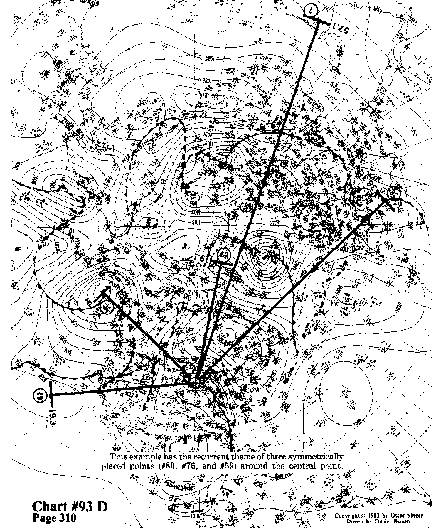
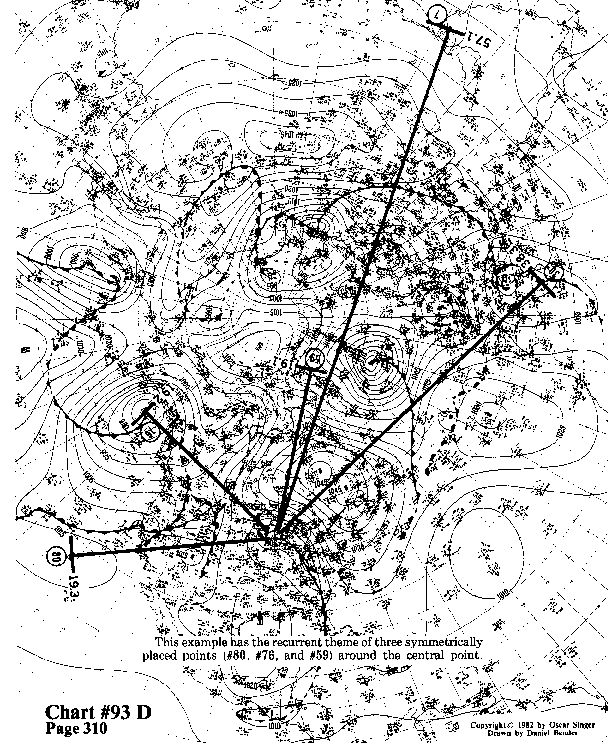
This example has the recurrent theme of three symmetrically placed
points (#80, #76, and #59) around the central point.