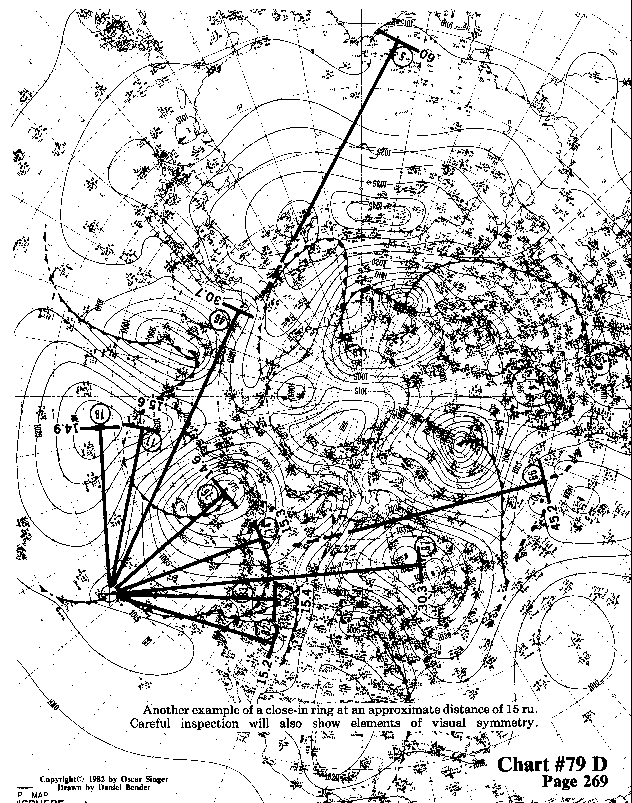
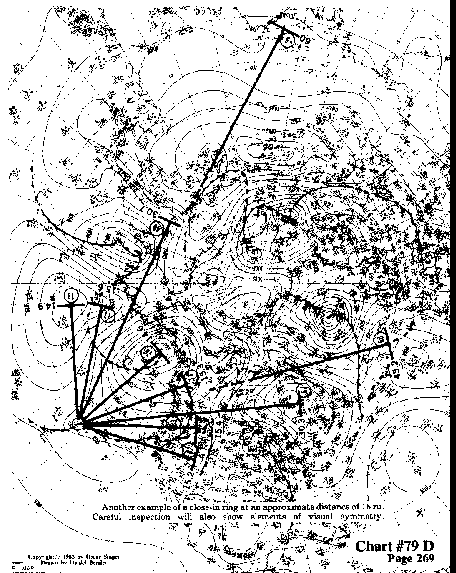
Another example of a close-in ring at an approximate distance of 16 ru. Careful inspection will also show elements of visual symmetry.

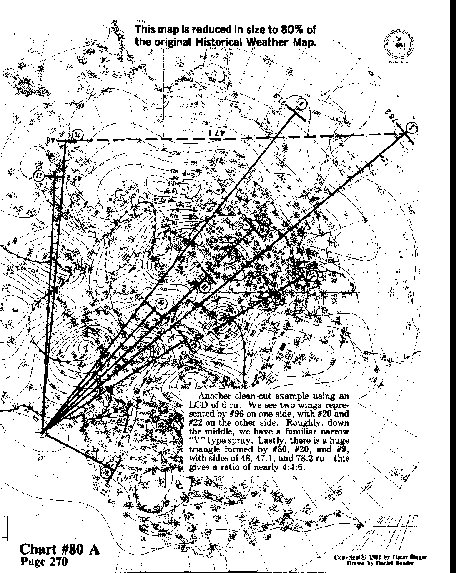
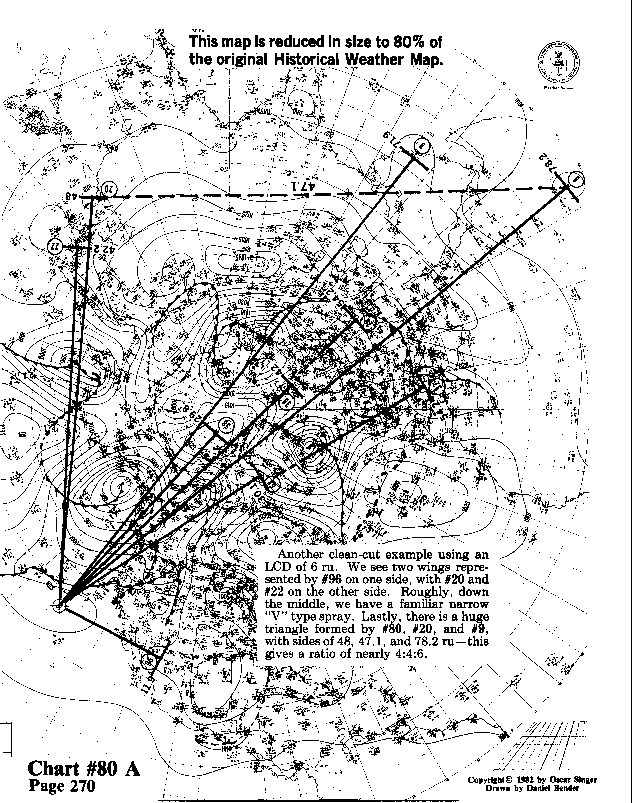
Another cleancut example using an LCD of 6 ru. We see two wings represented by #96 on one side, with #20 and #22 on the other side. Roughly, down the middle, we have a familiar narrow "V" type spray. Lastly, there is a huge triangle formed by #80, #20, and #9, with sides of 48, 47.1, and 78.2 ru--this gives a ratio of nearly 4:4:6.

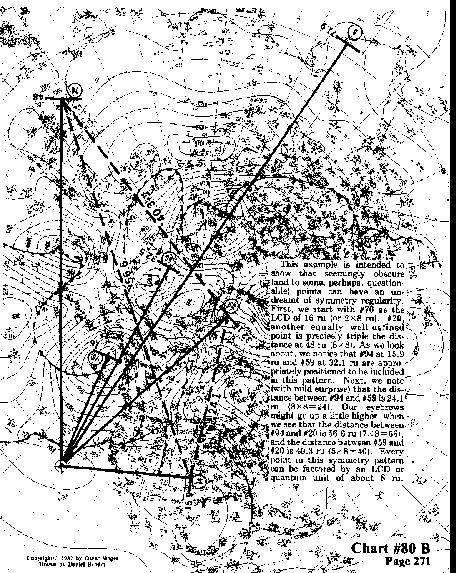
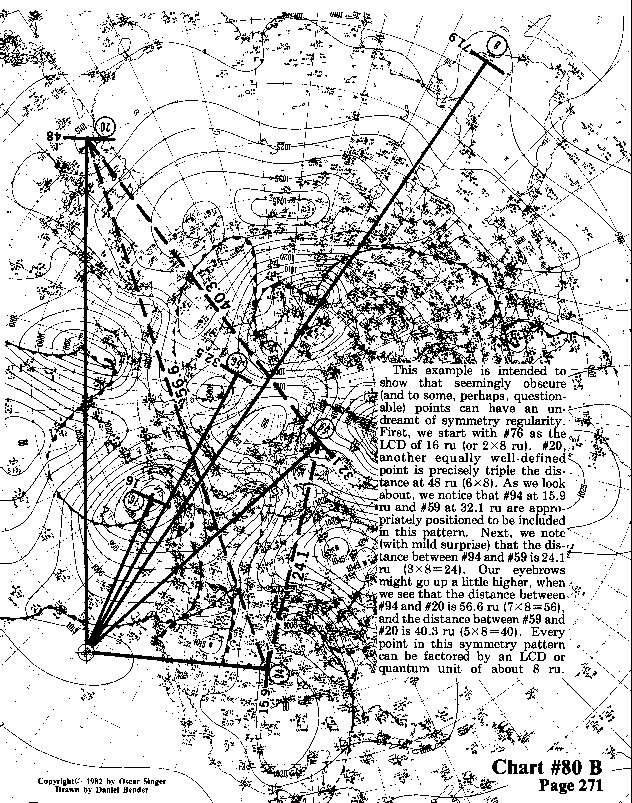
This example is intended to show that seemingly obscure (and to some, perhaps, questionable) points can have an undreamt of symmetry regularity .First, we start with #76 as the LCD of 16 ru (or 2x8 ru). #20, another equally well-defined. point is precisely triple the distance at 48 ru (6x8). As we look about, we notice that #94 at 15.9 ru and #59 at 32.1 ru are appropriately positioned to be included in this pattern. Next, we note (with mild surprise) that the distance between #94 and #59 is 24.1 ru (3 x 8 = 24) . Our eyebrows might go up a little higher, when we see that the distance between #94 and #20 is 56.6 ru (7 x 8 = 56), and the distance between #59 and #20 is 40.3 ru (5 x 8 = 40) . Every point in this symmetry pattern can be factored by an LCD or quantum unit of about 8 ru.

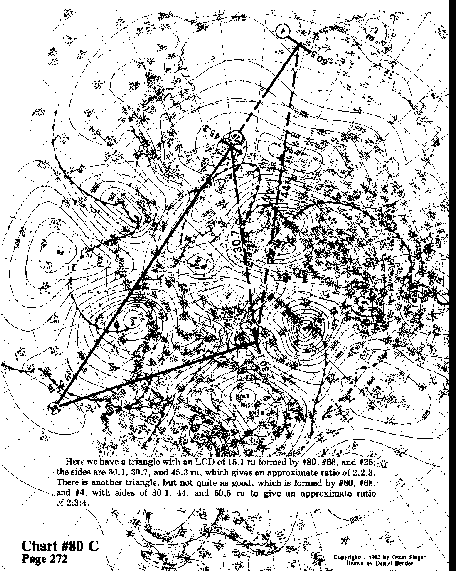
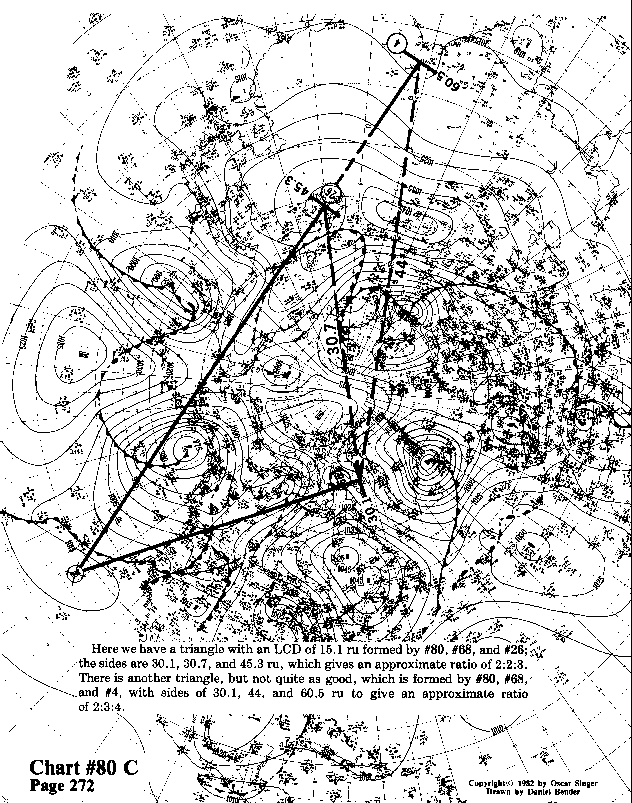
Here we have a triangle with an LCD of 15.1 ru formed by #80, #68, and #26; the sides are 30.1, 30.7, and 45.3 ru, which gives an approximate ratio of 2:2:3. There is another triangle, but not quite as good, which is formed by #80, #68, and #4, with sides of 30.1, 44, and 60.5 ru to give an approximate ratio of 2:3:4.

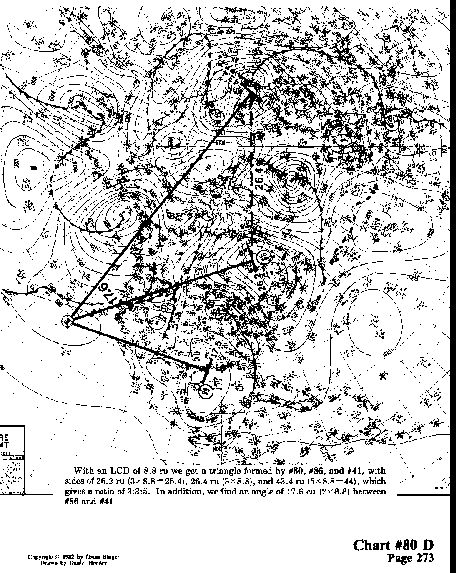
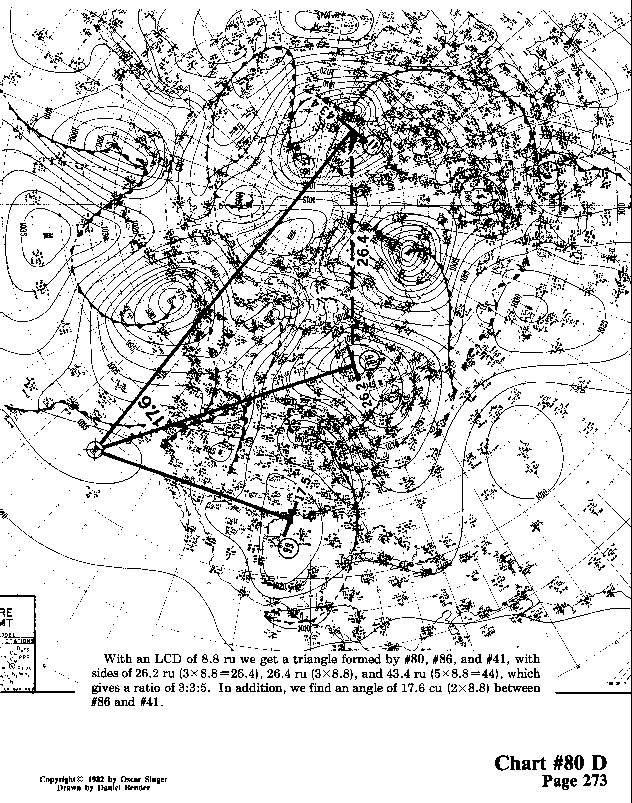
With an LCD of 8.8 ru we get a triangle formed by #80, #86, and #41, with sides of 26.2 ru (3 X 8.8 = 26.4), 26.4 ru (3 x 8.8), and 43.4 ru (5 x 8.8 = 44), which gives a ratio of 3:3:5. In addition, we find an angle of 17.6 cu (2 x 8.8) between #86 and #41.

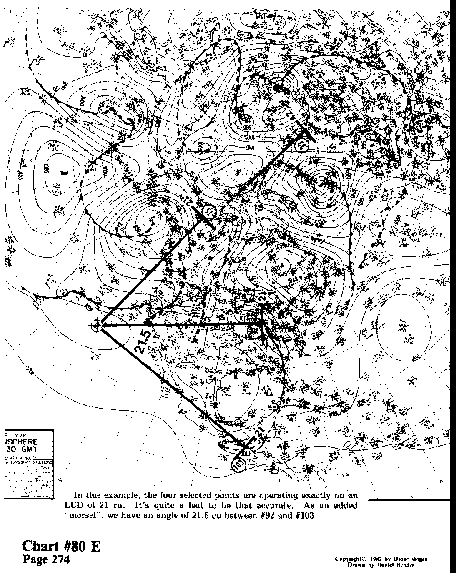
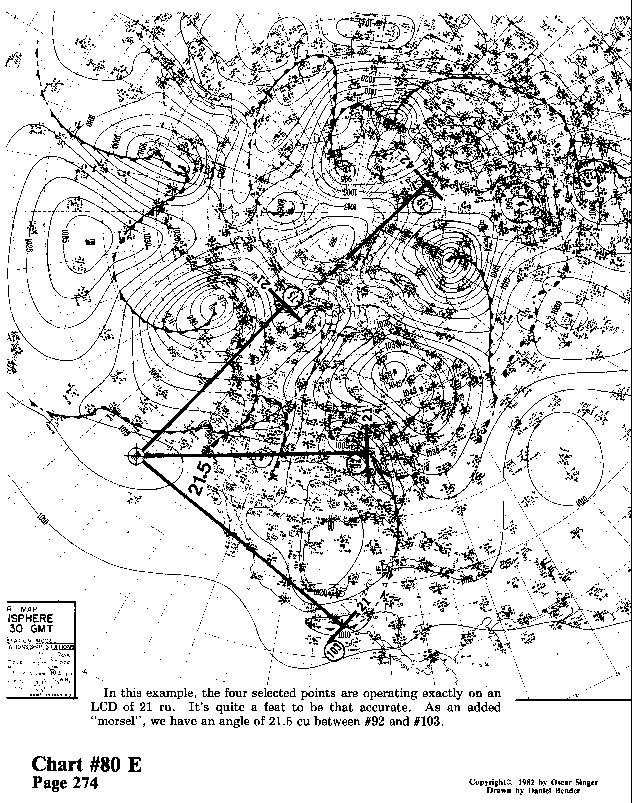
In this example, the four selected points are operating exactly on an LCD of 21 ru. It's quite a feat to be that accurate. As an added "morsel", we have an angle of 21.5 cu between #92 and #103.

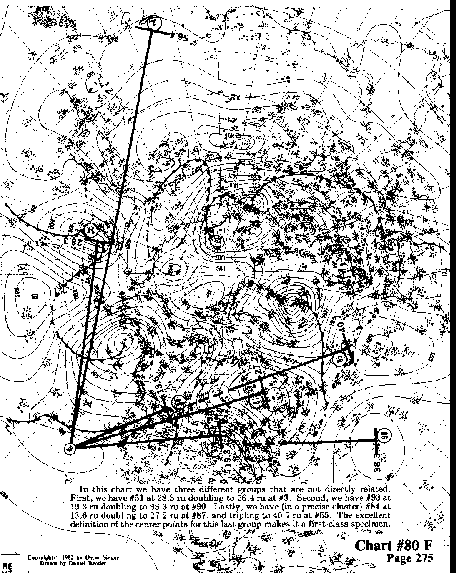
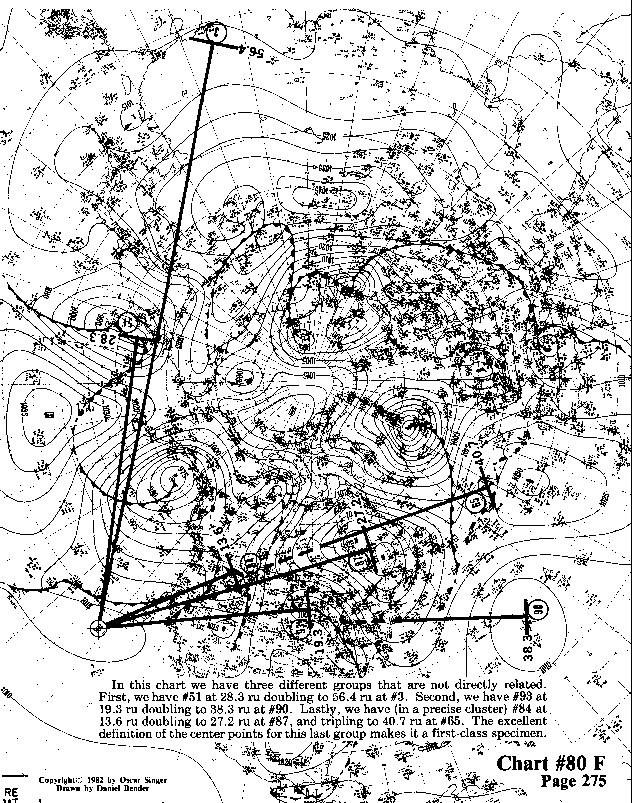
In this chart we have three different groups that are not directly related. First, we have #51 at 28.3 ru doubling to 56.4 ru at #3. Second, we have #93 at 19.3 ru doubling to 38.3 ru at #90. Lastly, we have (in a precise cluster) #84 at 13.6 ru doubling to 27.2 ru at #87, and tripling to 40.7 ru at #65. The excellent definition of the center points for this last group makes it a first-class specimen.

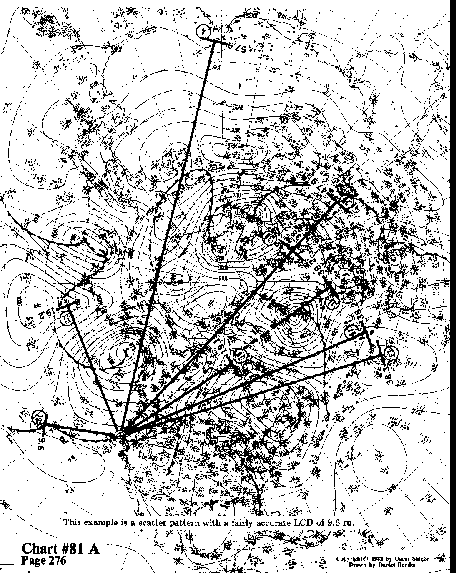
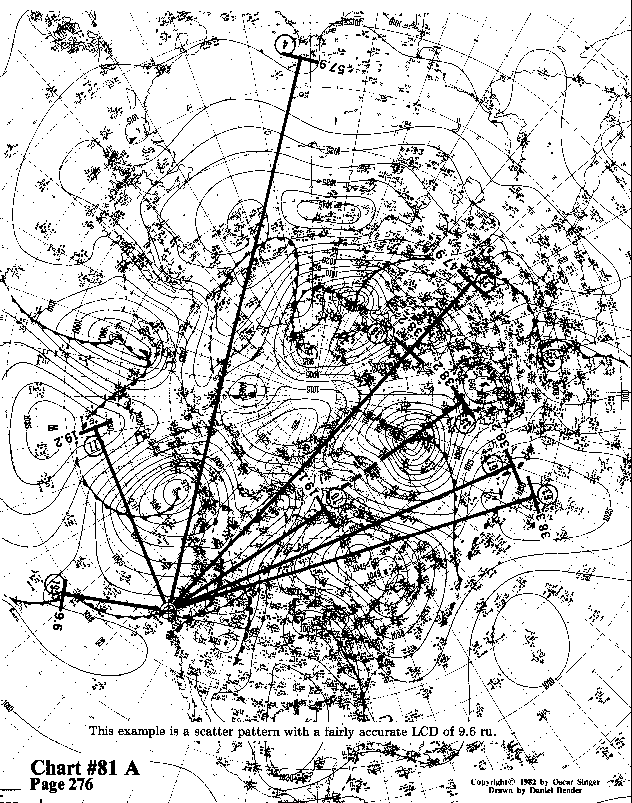
This example is a scatter pattern with a fairly accurate LCD of 9.6 ru.

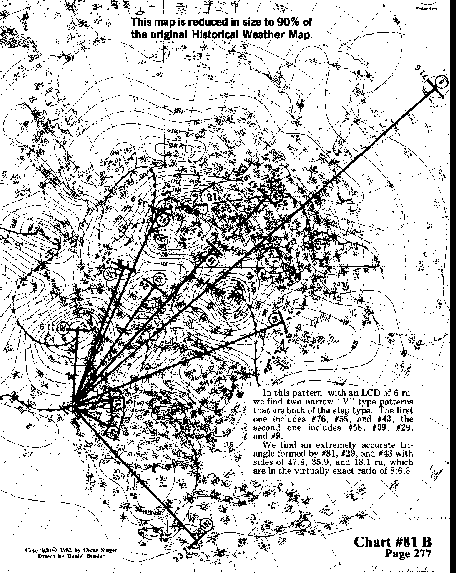
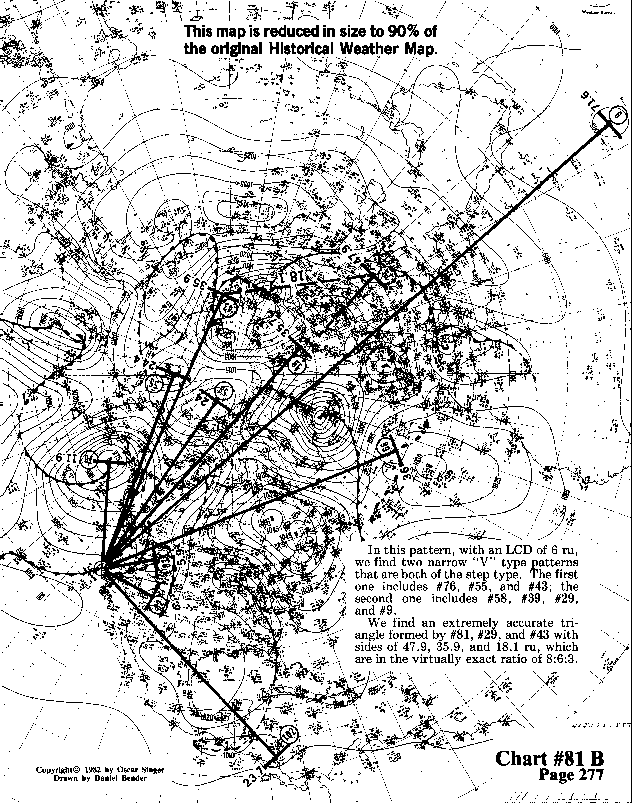
In this pattern, with an LCD of 6 ru, we find two narrow "V" type patterns that are both of the step type. The first one includes #76, #55, and #43; the second one includes #58, #39, #29, and #9.

We find an extremely accurate triangle formed by #81, #29, and #43 with sides of 47.9, 35.9, and 18.1 ru, which are in the virtually exact ratio of 8:6:3.

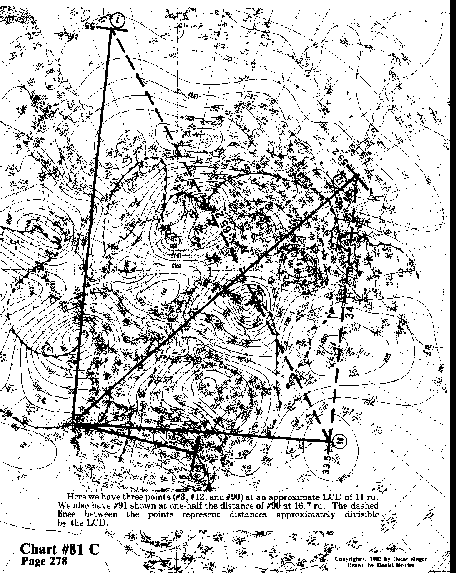
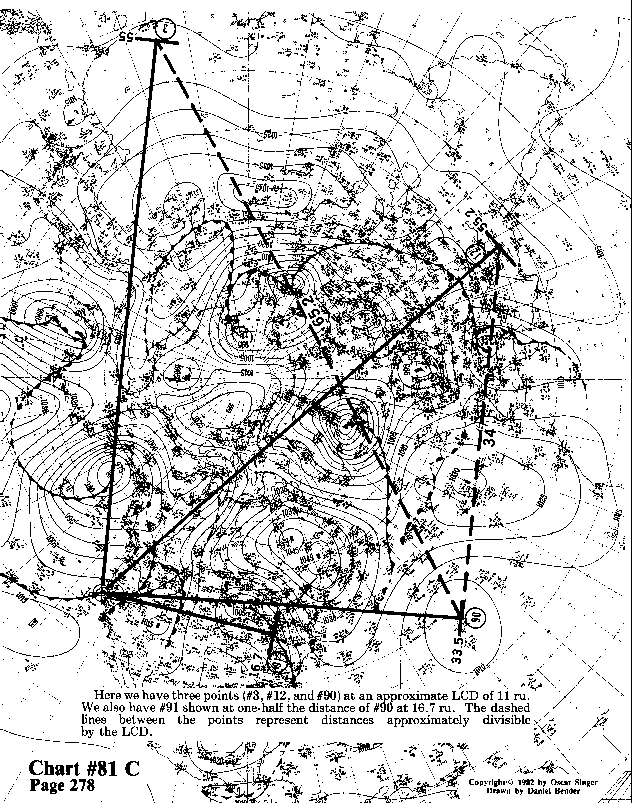
Here we have three points (#3, #12, and #90) at an approximate LCD of 11 ru. We also have #91 shown at one-half the distance of #90 at 16.7 ru. The dashed lines between the points represent distances approximately divisible by the LCD.

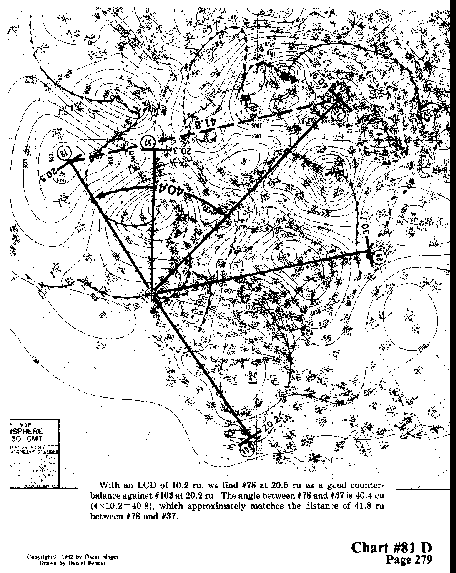
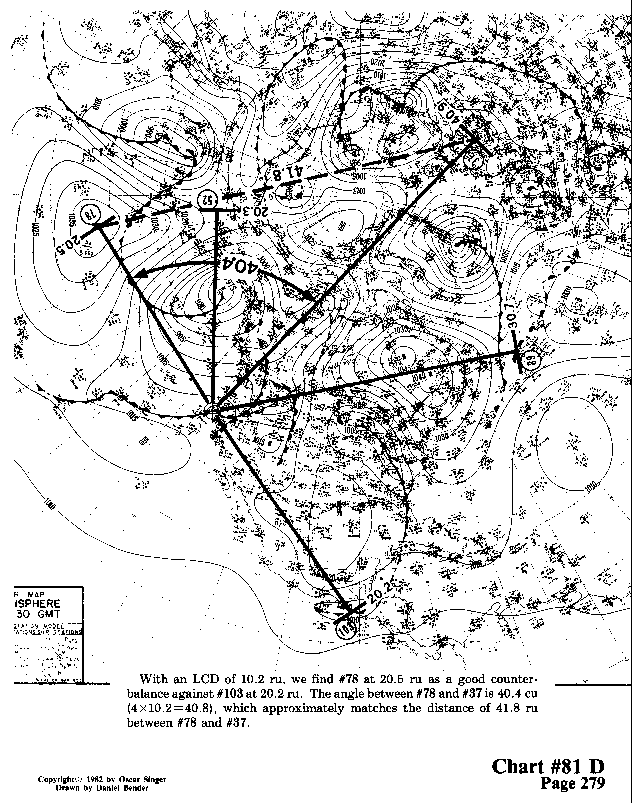
With an LCD of 10.2 ru, we find #78 at 20.5 ru as a good counterbalance against #103 at 20.2 ru. The angle between #78 and #37 is 40.4 cu. (4x10.2=40.8), which approximately matches the distance of 41.8 ru between #78 and #37.

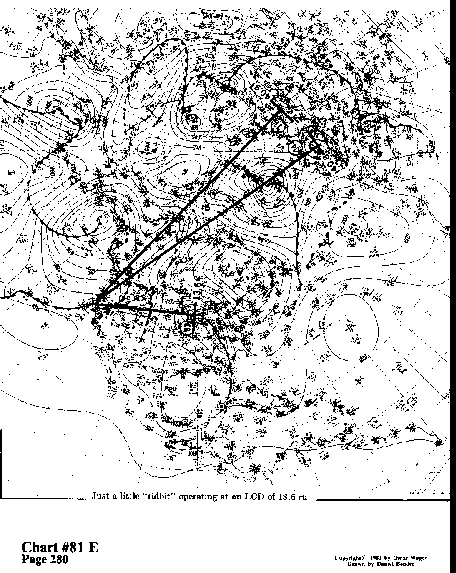
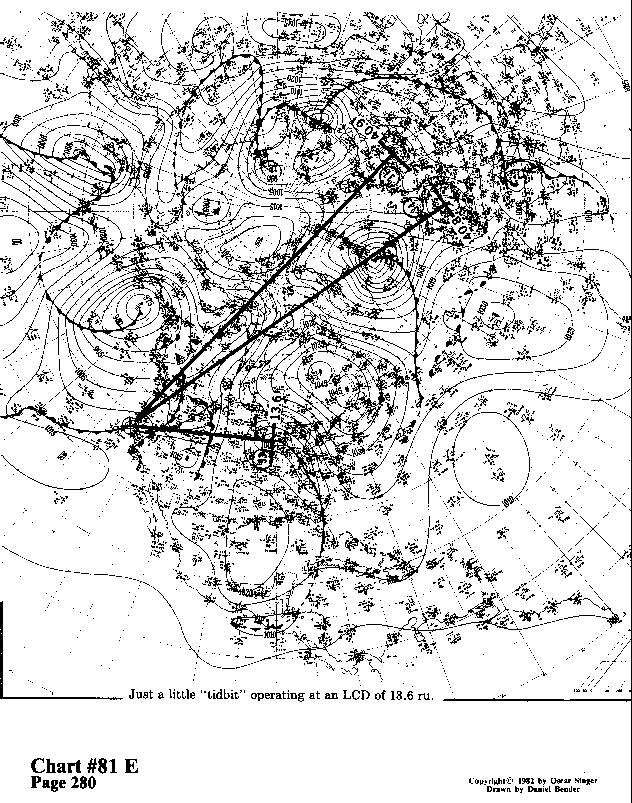
Just a little "tidbit" operating at an LCD of 13.6 ru.